Chapter 9

Synchronization and phase-locked loops

9.1 Introduction

In the previous chapter we laid out the basics of coherence theory as applies primarily to waves. Once inside the brain, the transduced sound no longer retains its wave characteristics, with the exception of its temporal properties that are synchronized to the external wave, either in carrier or in envelope. This enables a temporal continuity that applies to coherence, as is used in neurophysiological modeling. Specifically in hearing, carrier synchronization is mediated through the phase-locking process, which is possible at frequencies that are low enough for the neurons to track. What causes phase locking to appear in the auditory nerve pattern? This is usually not accounted for in cochlear mechanical models and is taken for granted in phenomenological models of the auditory nerve, whose input originates right at the synaptic interface between the inner hair cells (IHCs) and the auditory nerve. We would like to fill in this gap by showing that the organ of Corti and the outer hair cells (OHCs) can work as a phase-locked loop (PLL)—a circuit that synchronizes a local oscillator to an external source. As it turns out, different elements of the OHCs can assume the necessary components of a PLL—a phase detector that generates quadratic distortion components (\(f_2-f_1\)), a low-pass filter, and an oscillator that feeds back to the phase detector and serves as an output. While this model does not necessarily contradict the presently known or assumed functions of the OHCs (notably, amplification), it indicates that an important function of the OHCs may have been overlooked and that the cochlea and the auditory brain work in concert. In §16.4.2 we will additionally explore the possibility that efferent-mediated auditory accommodation has something to do with actively setting the PLL. In a narrower sense, though, the purpose of this chapter is to prove that external signal coherence can be conserved by the system, but not in an unconditional way.

In the next sections, we will review the general features of nonlinear synchronization in dynamical systems and specifically focus on PLLs. Then, a short proof of coherence conservation is sketched, using tools from the previous chapter. We will then quickly review the equivalence between a PLL and a general nonlinear oscillator, and draw parallels to known characteristics of the OHCs. We will then associate the different PLL components with known mechanisms in the OHCs, including some that are not so well understood that have not been well-accounted for in current models of the auditory system. We will finally consider potential evidence that can attest to some qualitative predictions that are made by the PLL model.

9.2 Background

Synchronization is a universal nonlinear phenomenon that applies to a very broad class of systems in the natural world and in engineering. It occurs when the oscillations or rhythms of two or more independent systems adjust to one another due to (weak) coupling between them (Pikovsky and Kurths, 2001). It is critically distinguished from systems that contain a resonant component that would not oscillate on its own (i.e., it does not have an internal energy source). It is also distinguished from systems that are coupled so rigidly that they effectively become one, which means that the output phase of the forced system is tightly determined by the input. Hence, the response of two synchronized oscillators does not behave like a resonant filter, even if the two outputs appear to be the same under certain conditions.

Noun	Adjective
synchronization	synchronized
(phase) synchrony/synchronicity	synchronous
entrainment	entrained
phase locking, phaselock	phase-locked, locked
frequency locking	frequency-locked
mode locking	mode-locked
coherence, coherency	coherent
correlation	correlated
coincidence	coincident

Table 9.1: A list of near-synonyms that relate to the concept of synchronization. The differences in meaning are generally subtle and not always consistent between different texts and authors. Specific meanings that are employed in this work are defined in the text.

The first documented synchronized systems were originally discovered in mechanics and later in acoustics. The discovery of mode locking is attributed to Huygens, who patented the pendulum clock in 1656 and found out that the pendulum motion of two clocks hanging from the same wooden beam became tightly synchronized, only in anti-phase, due to imperceptible coupling through the beam (Pikovsky and Kurths, 2001). More than two centuries later, Rayleigh observed that when the ends of two organ pipes that are slightly mistuned are brought close together, they tend to resonate in unison, instead of beating slowly together (Rayleigh, 1879b; Rayleigh, 1945; p. 322c; Gripon, 1874; see also,][ for an even earlier account; additionally, see Abel et al., 2006 for modern measurements and model). Effectively, the fundamental modes of the two pipes become locked when the difference in their resonance frequencies is small and when the pipes are closely positioned. Using more precise measurement tools, Rayleigh (1907a) also found a very similar effect in two vibrating tuning forks that are slightly detuned, even when their coupling was very weak—through the air, or with a thin cotton thread.

Further notable discoveries of synchronization effects were mainly in electronic circuits with coupled oscillators (Vincent, 1919; Eccles and Vincent, 1920; Appleton, 1922; van der Pol, 1926). The associated electronic principles were critical in applied communication engineering and therefore received much theoretical attention subsequently. Many other phenomena in different domains (e.g., chemical, ecological) have been identified since (see Pikovsky and Kurths, 2001 for a review and further bibliography).

A more general type of synchronization can take place within a single oscillator that has multiple normal modes or coupled oscillators with different frequencies. Such higher-order synchronization between different modes is relatively general and can occur when the natural frequencies of two coupled systems are nearly harmonically related (Pikovsky and Kurths, 2001; p. 104):

\[ n\omega_1 \approx m\omega_2 \]

(9.1)

where \(n\) and \(m\) are two integers and \(\omega_1\) and \(\omega_2\) are angular frequencies. Thus, even though few real-world vibrating objects are precisely harmonic, it is theoretically possible to induce nearly-harmonic modes to vibrate harmonically by coupling the objects together. By virtue of nonlinear mode-locking, musical instruments that produce sustained notes often end up producing harmonic sound under certain conditions (Fletcher and Rossing, 1998; pp. 143–144). It is difficult to estimate how prevalent these conditions may be encountered in real life, though, as they are rather restrictive (see §3.3.1 for more details and examples).

Synchronization phenomena consist of numerous systems and a very rich set of effects and methods that appear in diverse contexts. We would like to focus on one particularly influential system, the phase-locked loop (PLL), which encapsulates some of these effects in a way that can be applied to hearing, without loss of generality. In addition to being a powerful model with high explanatory power, the PLL also provides a biomechanical and neurophysiological link to the signal coherence arriving from the environment, as was described in the previous chapter.

9.3 The phase-locked loop (PLL)

In the following, the principles of operation of the PLL, its main applications, and some of its key specifications and limitations are going to be briefly reviewed, based on texts by Wolaver (1991), Stephens (2001), Margaris (2004), Gardner (2005) as well as a short introduction in Couch II (2013, pp. 282–290).

One of the most common requirements in communication systems and in numerous other electronic systems is to force a local oscillator to track the instantaneous phase variations of an external (reference) signal. The PLL is perhaps the most common device that achieves this function. It has had a century-long history in modern electronic engineering and control theory (Stephens, 2001; pp. 1–9). It is not an overstatement to say that the fidelity of modern communication technology would have been impossible without the invention and perfection of the PLL, which enables the synchronization of receivers to transmitters at arbitrary distances, frequency channels, and modulation techniques, often in prohibitive noise conditions.

The most basic PLL architecture can appear deceptively simple—it consists of an external signal fed into a phase detector that is connected to a local oscillator, which is itself connected by a feedback loop back to the phase detector (Figure 9.1). The fed back signal ensures that the phase detector output works as a correction control signal that always keeps the oscillator locked to the input. The phase detector is by definition a nonlinear device, where the difference between the input and the fed-back output is one of its distortion products. The instantaneous difference between the two signals corresponds to their phase difference. The PLL typically contains an additional low-pass filter that removes any high-frequency distortion products that are not needed by the oscillator. More importantly, the filter can determine the dynamical properties of the PLL—its stability and frequency response. This basic architecture can be complexified to any degree necessary and there are numerous ways to implement it in practice, both in analog and in digital electronic systems.

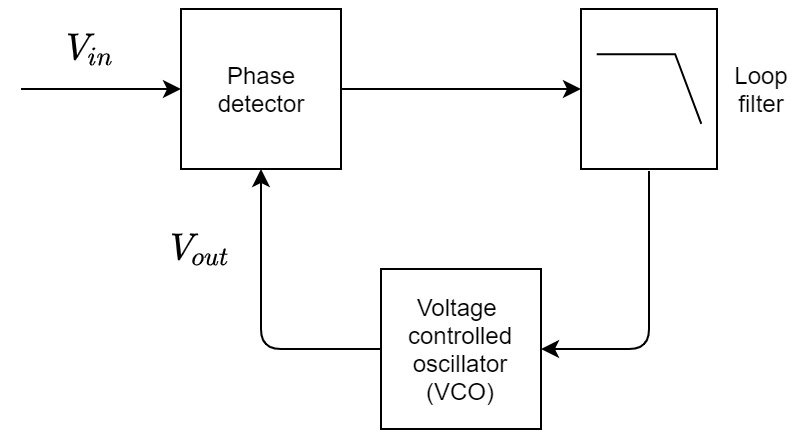
Figure 9.1: The basic elements of a phase locked loop (PLL).

The PLL is considered “locked” when the phase difference is zero (or constant). In reality, even in the locked state there is a finite steady-state phase error, which fluctuates around zero. This can often make the locked PLL appear as a narrowband filter that is capable of rejecting much of the noise, especially if the signal is well-behaved (e.g., Gardner, 2005, p. 2). Since the frequency is the derivative of the phase, phaselock entails (instantaneous) frequency-lock as well.

Different frequency ranges and characteristic time constants are associated with the PLL operation. A PLL in lock can only remain so within the hold-in range—the maximum bandwidth around the carrier frequency in which the PLL works. If, however, the signal frequency changes quickly yet gradually, the PLL may not be able to maintain lock and its phase error will increase. However, as long as the change is within the pull-in range, which is narrower than the hold-in range, then the PLL will be able to reacquire its lock slowly through a pull-in process. Similarly, if the input signal frequency is changed abruptly (i.e., with a frequency step), the PLL will not be able to retain its lock if the step breaches the pull-out range, which is narrower than the pull-in range. Finally, the lock range (also, the capture range) is the narrowest of the PLL ranges and is where it can quickly achieve lock to input signal changes—without a single beat note—in what is called the lock-in process. The different frequency ranges associated with the PLL are illustrated in Figure 9.2. Care must be taken in the design of the PLL to not make its lock range too narrow, because it can result in excessive increase of the pull-in time, as tracking a fluctuating signal becomes more difficult.

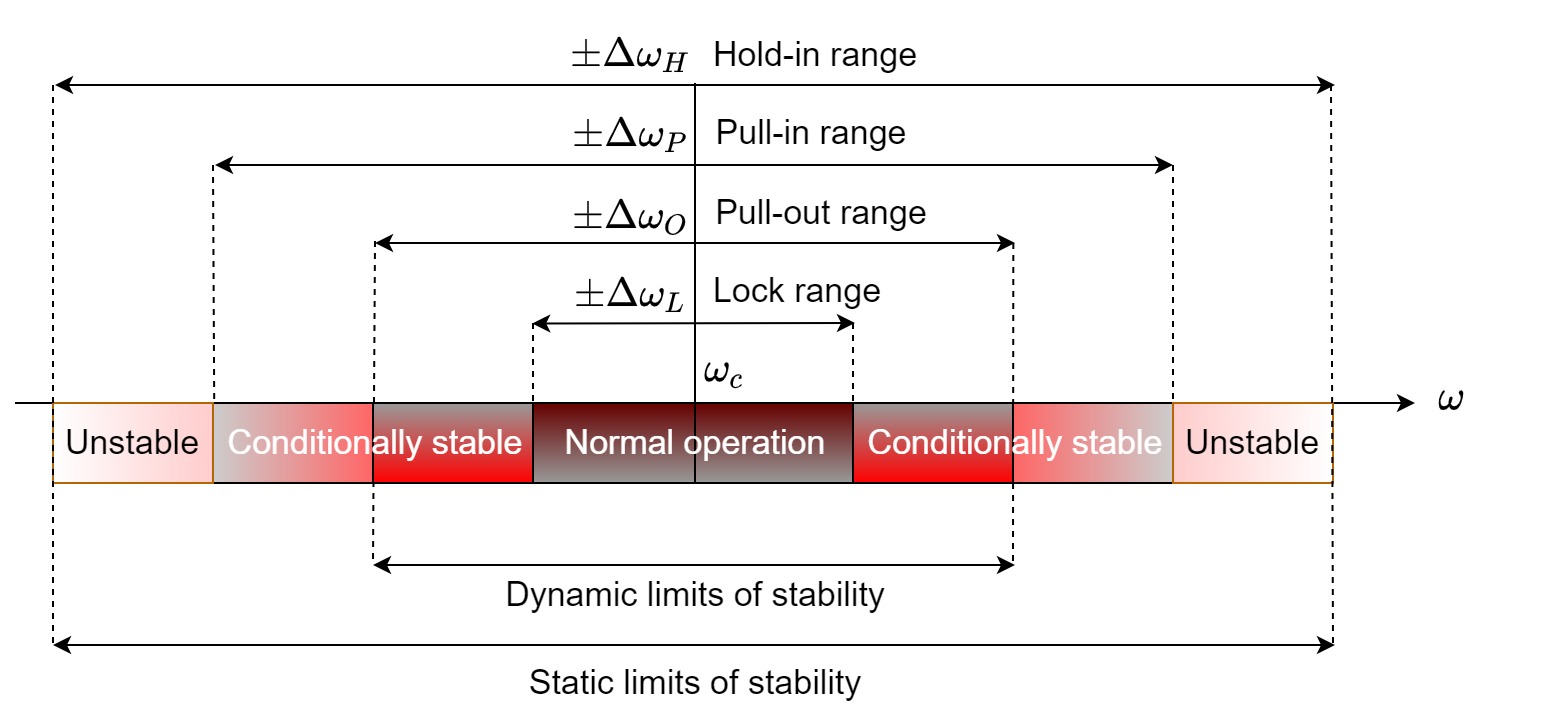
Figure 9.2: The four basic frequency ranges of the PLL, which characterize its operating range and typical dynamic stability. This illustration is based on Figure 2.29 in Best (2003).

The phase detector is a nonlinear device that produces a distortion product that is proportional to the phase difference of its two input signals. In simple analog designs, it is modeled as an ideal mixer, or a multiplier, where it is made clear that it produces the sum and the difference of the two input signal frequencies. The sum is of no use and is removed by the loop filter to avoid adding noise to the control signal of the oscillator. Real phase detectors are also characterized by a ripple response that is superimposed on their phase difference output function.

The PLL oscillator has to have a tunable frequency, typically achieved using a DC voltage control-signal, giving it the name voltage-controlled oscillator (VCO). The control signal is biased along with the error signal from the phase detector, which results in the dynamic tuning of the VCO frequency. The oscillator is inherently a nonlinear device as well, although in linear treatments of PLL theory it is modeled as an ideal integrator with stable tuning. This alludes to one of the main motivations for having a PLL in the first place—all oscillators (and clocks) tend to drift, so if left uncontrolled, they lose their tuning over time in an unpredictable way (e.g., Eccles and Vincent, 1920). In coherent demodulation tasks such a drift is particularly detrimental, because it leads to an accumulated phase noise in the demodulated product, which amounts to distortion and reduced signal-to-noise ratio (SNR) at the output. Another nonlinear property of oscillators is their tendency to phase-lock to directly injected signals (i.e., in the case of a PLL, not via the phase detector and filter). This tendency can disrupt the controlled operation of the full PLL and is therefore kept to a minimum by design.

The loop filter, generally low-pass, is placed between the phase detector and oscillator, but might be altogether absent in the most primitive designs. The loop filter is critical in determining the stability characteristics of the PLL—the susceptibility for self-oscillation or inability to pull out of the locked position, as the feedback loop becomes positive. The order of the filter determines the order of the PLL itself plus one. For example, a second-order low-pass filter makes for a third-order PLL⁸³. In simple first-order PLLs, there is a single parameter that can be optimized (gain). However, first-order PLLs are inadequate in most applications, as they cannot lock to arbitrary signal types. Increasing the filter order provides the circuit designer with additional parameters that can be better tailored to achieve certain tasks. For example, a third-order PLL is better-suited to maintain lock to the received signal despite relative motion of the transmitter, which induces a Doppler shift on its spectrum. Similarly, only third-order PLLs can track a linear frequency modulation ramp. Third-order is also typically used for frequency synthesis, which is another common application for PLLs. However, in second- and third-order PLLs there is a risk of instability as the poles may be sensitive to gain and input level changes. PLLs of higher order than three are uncommon in typical applications.

9.4 The linearized PLL model

The PLL equations are not going to be used explicitly in this work, but they are presented because of the valuable insight that they provide for the understanding of the PLL principles of operation.

Several different models have been developed that describe the PLL operation. Of them, the linearized model of the PLL is the simplest to derive—as it requires only one approximation in the nonlinear equations. It preserves sufficient complexity that captures the central aspects of the PLL operation, which is completely satisfactory in steady-state conditions. It is the transient behavior—mainly pulling in (acquiring lock) and pulling out—that is manifestly nonlinear and sometimes requires other analytic methods. The linearized PLL model derivation is reproduced below, originally developed by Jaffe and Rechtin (1955) and elaborated by others. A nonlinear approach that accounts for the transient behavior of the PLL is given in Margaris (2004).

For a system that is described in Figure 9.1, let us assume a reference input signal around a carrier \(\omega_c\) with an arbitrary phase function \(\varphi_i(t)\) and amplitude \(\sqrt{2} A_i\)

\[ V_{i}(t) = \sqrt{2} A_i \sin \left[ \omega_c t + \varphi_i(t) \right] \]

(9.2)

The output from the VCO is chosen to be in quadrature, with an output phase function \(\varphi_o(t)\) and amplitude \(\sqrt{2} A_o\)

\[ V_{o}(t) = \sqrt{2} A_o \cos \left[ \omega_c t + \varphi_o(t) \right] \]

(9.3)

where the instantaneous phase function of the VCO is determined by its voltage input \(V_o(t)\)

\[ \varphi_o(t) = K_v\int _{-\infty}^t V_o(\tau)d\tau \]

(9.4)

with \(K_v\) being the gain of the VCO. We can express the same relation in differential form

\[ \frac{d\varphi_o(t)}{dt} = K_v V_o(t) \]

(9.5)

which directly quantifies the sensitivity of the VCO output voltage to the change in the instantaneous frequency of the input.

Both \(V_{i}\) and \(V_o\) are inputs to the phase detector, whose operation is to multiply them with sensitivity \(K_m\). Because we selected the reference and VCO to be in quadrature, their sum and difference terms are both sine functions

\[ V_d(t) = 2K_m A_o A_i \sin \left[ \omega_c t + \varphi_i(t) \right]\cos \left[ \omega_c t + \varphi_o(t) \right]\\ = K_m A_o A_i \left\{ \sin \varphi_e (t)+ \sin \left[ 2\omega_c t +\varphi_o(t) + \varphi_i(t) \right] \right\} \]

(9.6)

where we defined the difference phase to be the phase error,

\[ \varphi_e(t) \equiv \varphi_i(t) -\varphi_o(t) \]

(9.7)

which is zero when the PLL is locked in, by definition. Next, we assume that the low-pass loop filter removes the sum term on the right of Eq. 9.6, and that the remaining difference term is convolved with the impulse response of the filter \(h_f(t)\)

\[ V_c(t) = K_m A_o A_i \sin \varphi_e(t) * h_f(t) \]

(9.8)

that yields the output signal \(V_c(t)\) from the filter, which is the input to the VCO that scales it by a gain \(K_v\) (Eq. 9.5), as by definition, the output phase of the VCO is proportional to its input. Thus, we can now construct an integro-differential equation for \(\varphi_e(t)\) by differentiating Eq. 9.7

\[ \frac{\varphi_e(t)}{dt} = \frac{\varphi_i(t)}{dt} - K_v K_m A_o A_i \int_0^t \sin\varphi_e(\tau)h_f(t-\tau)d\tau \]

(9.9)

This is the basic nonlinear equation that describes the PLL, but it does not have a closed-form solution without some approximations. The linearized solution approach has the sine function approximated for small angles with

\[ \sin\varphi_e(t) \approx \varphi_e(t) \]

(9.10)

just like in the paraxial optics approximation of geometrical optics (§4.2.1).

Without explicitly solving it, we can find the theoretical hold-in frequency range around \(\omega_c\) for which the PLL can maintain its lock. If the input frequency \(d\varphi_i(t)/dt\) is changed infinitesimally slowly, then the low-pass filter response can be approximated to its DC gain, \(K_f\). Using the definition of \(\varphi_e(t)\), Eq. 9.9 can be rewritten as

\[ \frac{d\varphi_o(t)}{dt} = K_v K_m K_f A_o A_i \sin\varphi_e(t) \]

(9.11)

Eq. 9.11 is maximized for \(\sin\varphi_e(t) = \pm 1\), and we can obtain the maximum frequency range,

\[ \Delta \omega_h = K A_o A_i \]

(9.12)

where we compacted all the gain constants into a single symbol \(K\)

\[ K = K_v K_m K_f \]

(9.13)

which is called the loop gain of the PLL. \(K\) is also called the PLL bandwidth. In the first-order PLL, the bandwidth is equal to the hold-in, pull-in, pull-out, and lock ranges, so \(K = \omega_h\). All PLL orders fundamentally depend on the loop gain \(K\) (Gardner, 2005; pp. 20–22).

The simplest time-domain solution to Eq. 9.9 can be obtained for an ideal filter with pure attenuation (or gain) and no zeros or poles, so that \(h(t) = K_f\delta(t)\). Using the linear approximation, this leaves us with a first-order PLL

\[ \frac{\varphi_e(t)}{dt} = \frac{\varphi_i(t)}{dt} - K A_o A_i \varphi_e(t) \]

(9.14)

which has closed-form solutions for specific input types (e.g., Stephens, 2001, pp. 16–19).

In the linear approximation, the transfer function of the PLL exists, and it is possible to analyze the closed-loop circuit in the frequency domain using the Laplace transform. The most useful closed-loop transfer function is a phase function ratio

\[ H(s) = \frac{\Phi_o(s)}{\Phi_i(s)} = \frac{K_v K_m A_o A_i H(s)}{s + K_v K_m A_o A_i H(s)} \]

(9.15)

where \(s\) is the Laplace-transform complex frequency variable, which can be set to \(s = i\omega\) to convert it to standard frequency. For the first-order PLL, this expression simplifies to

\[ H(\omega) = \frac{K A_o A_i}{i\omega + K A_o A_i} \]

(9.16)

which is a low-pass response and is unconditionally stable. In the majority of situations, this design is impractical, as it requires high gain in order to achieve lock, which directly increases the bandwidth of the PLL (Eq. 9.12) and hence the susceptibility to noise. Also, it is often the case that a spurious pole (e.g., a delay) appears in the loop as a result of the phase detector, for example, which would then make it unstable when combined with high gain. With low gain this PLL would be unable to maintain lock for most variable signals, so a more sophisticated filter is required in almost all applications, namely, a second- or third-order PLL. It is important to note that the PLL response varies with the level of the reference input (and its SNR), which makes the PLL highly nonlinear. For this reason, some designs try to stabilize or compress the input level, or design an appropriate filter to minimize this dependence (Jaffe and Rechtin, 1955).

Basic examples for the responses of three simple PLL topologies are displayed in Figure 9.3. The numerical values were selected to exaggerate the duration of the transient responses, so it should not be implied that these values are representative of real-world designs. The damping factor in the filters of the second-order PLLs was chosen to be 0.707 as an ideal trade-off between filter ringing and damping. All PLL topologies would acquire lock more quickly with higher bandwidth and/or gain, as long as they are not overdamped or underdamped. Note how all PLLs are able to track the frequency step successfully, but only the second-order PLL with an integrator can (almost) track the linear chirp. Also, before locking onto the frequency step, the second-order type 1 PLL (bottom left of Figure 9.3 in blue) phase-slips and misses about one cycle—a common PLL characteristic during lock, which is tantamount to an error.

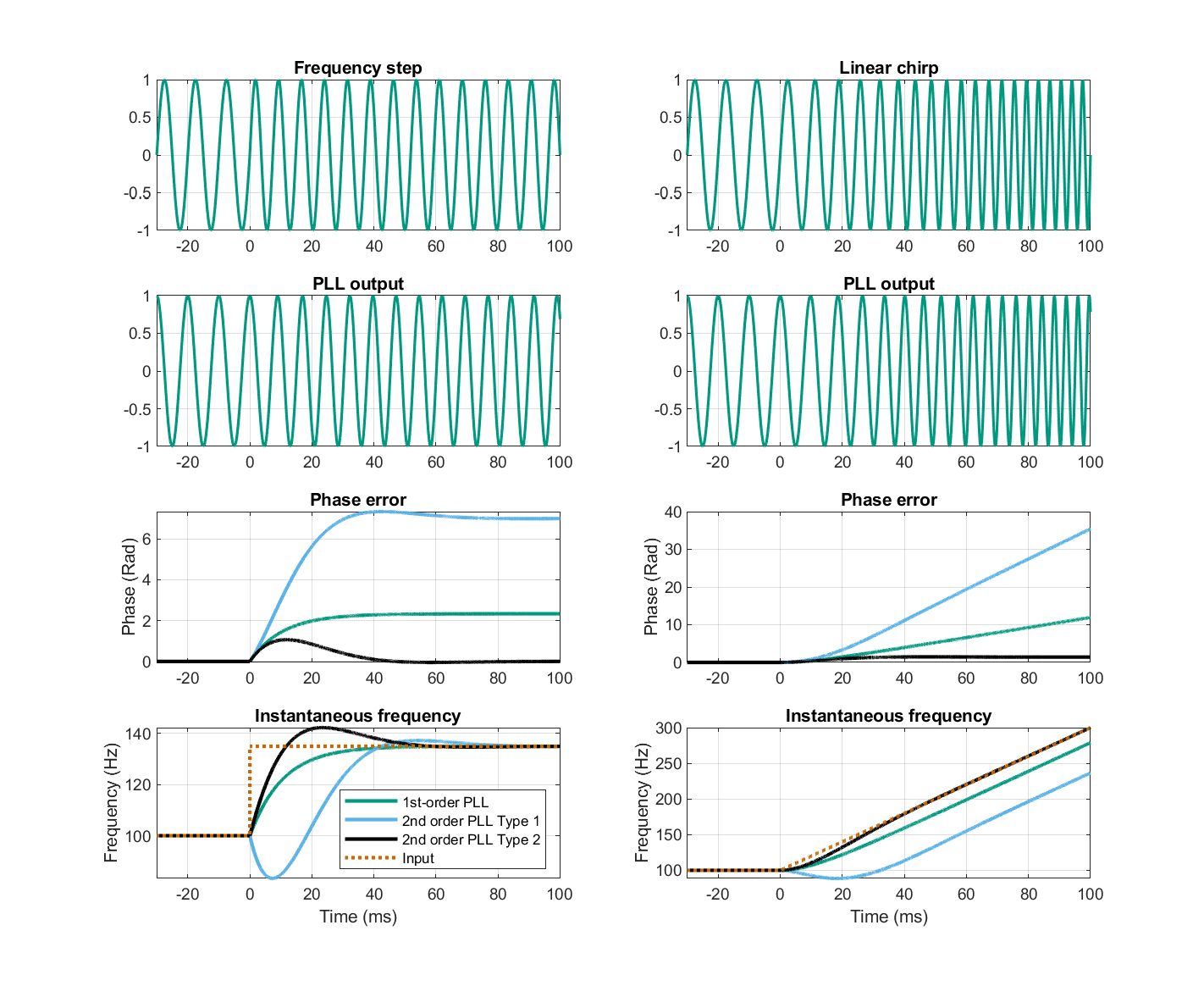
Figure 9.3: Examples of linearized phase-detector (\(\sin\varphi_e(t) \approx \varphi_e(t)\)) PLL responses to frequency step of +35 Hz (left) and frequency linear chirp of 4000 Hz/s (right) starting at \(t=0\), from a constant frequency at \(t<0\) of 100 Hz. The output responses (second row) are from the first-order PLL as follows. The responses of three basic PLL topologies are shown in the bottom two rows: first-order PLL with \(K = 15\) Hz (green curves); second-order PLL type 1 with \(f_n = 35\) Hz, \(\zeta = 0.707\), \(K_v = 5\), low-pass with lead compensation filter, \(F(s) = K_v\frac{1+s\tau_2}{1+s\tau_1}\) with \(\tau_1 = \frac{K_v}{(2\pi f_n)^2}\), \(\tau_2 = \frac{2\zeta}{2\pi f_n}\left( 1 - \frac{2\pi f_n}{2K\zeta} \right)\) (blue curves); and second-order PLL type 2, \(f_n = 35\) Hz, \(\zeta = 0.707\), an integrator and lead compensation \(F(s) = \frac{1+s\tau_2}{s\tau_1}\) with \(K = 4\pi\zeta f_n\), \(\tau_2 = \frac{\zeta}{\pi f_n}\) (black curves). The simulation is based on a Matlab code by Mark Wickert, 2014, http://ece.uccs.edu/~mwickert/ece5675/lecture_notes/PLL_simulation.pdf.

The PLL operation is susceptible to poor SNR, which translates to phase noise in the phase detector that increases the error, increases the pull-in time, and decreases the hold-in, pull-in and other frequency ranges. The phase error dependence on SNR is generally nonlinear—it is almost unaffected at positive SNRs, but deteriorates quickly at around 0 SNR. In a narrowband channel with bandlimited Gaussian noise, the effect of noise is well-modeled as equivalent to being added from within the loop rather than through the phase detector input. This means that the noise translates to additive phase noise inside the PLL. However, the internal SNR in the loop is actually 3 dB better than the external one in the input. Additionally, just as the loop performance depends on the signal level, so does the phase detector gain may depend on the SNR. It is possible to mitigate the noise effects by correctly designing the loop filter, so that the phase error is minimal for given SNR and input level, e.g., by decreasing the bandwidth when the SNR is low. It should be noted that internal noise generated by any of the PLL components may be significant and has to be considered as part of the total noise model. It is sometimes useful to refer to the noise-equivalent bandwidth \(B_n\), which can be computed from the closed-loop transfer function (Eq. 9.15) with

\[ B_n = \frac{1}{2\pi} \int_0^{\infty}|H(\omega)|^2 d\omega = \frac{K A_o A_i}{4} \,\,\,\ (\mathop{\mathrm{Hz}}) \]

(9.17)

for a first-order PLL. This expression and the bandwidth \(\Delta \omega_h\) become more complicated for higher-order PLLs.

9.5 PLL coherence

It is a convention in communication theory that employing a PLL in the circuit enables coherent detection (§5.3.1). Therefore, as a corollary to the PLL basic function, we would also like to find out under what conditions a PLL can conserve the arbitrary coherence properties of an input signal. The phase detector continuously compares the input and output signals by multiplying them (Eq. 9.6), so it can be thought of as a correlator, which produces the instantaneous cross-term of the coherence function. The coherence function is therefore expected to be dependent on the phase error between the input and the output.

Let us inspect a narrowband input of the form

\[ p_i(t) = A(t)\exp \left\{ i[\omega_c t +\varphi(t)] \right\} \]

(9.18)

The input can be described by its (nonstationary) self-coherence function, \(\gamma_{ii}(t,\tau)\). Without loss of generality, the output signal is the same but is amplified with gain \(B(t)\), and differs from \(p_i(t)\) by the instantaneous phase error \(\varphi_e(t)\)

\[ p_o(t) = B(t)A(t)\exp \left\{ i[\omega_c t +\varphi(t) + \varphi_e(t)]\right\} \]

(9.19)

The corresponding self-coherence function of the output is then \(\gamma_{oo}(t,\tau)\).

Assuming that the gain varies very slowly in time compared to the phase tracking operation, we assume that \(B(t) \approx \mathop{\mathrm{const}}\), so we can use normalized amplitudes and the normalized coherence function \(\gamma_{io}\) instead of \(\Gamma_{io}\) (see §8.2.1 for definitions). According to Eq. §8.72, the nonstationary coherence function is given by

\[ \gamma_{io}(t,\tau) = \frac{1}{N}\sum_{n=1}^N p_i^*(t_n)p_o(t_n + \tau) \]

(9.20)

where we substituted, for simplicity, \(t=t_1\) and \(\tau=t_2-t_1\), in Eq. §8.72, which corresponds to the update (processing) time of the feedback loop of the PLL⁸⁴. Each time instance \(t_n\) may relate to a period in which the input self-coherence function is more or less stable. We examine only the low-frequency terms of the coherence function and neglect the fast-varying terms in the sum

\[ \gamma_{io}(t , \tau) = \frac{1}{N}\sum_{n=1}^N \exp\left\{ i[\omega_c \tau + \varphi(t_n +\tau) - \varphi(t_n) + \varphi_e(t_n + \tau)] \right\}\\ = \frac{\exp( i\omega_c \tau)}{N}\sum_{n=1}^N \exp\left\{ i[\varphi(t_n +\tau) - \varphi(t_n) + \varphi_e(t_n + \tau)] \right\} \]

(9.21)

where the constant difference in the carrier phase was taken out of the sum and has no effect on the magnitude of the coherence function.

There are three phase terms in the argument of the exponential in the sum of 9.21. The first two, \(\exp\left[\varphi(t_n + \tau) - \varphi(t_n)\right]\), are equivalent to the autocorrelation function of the signal \(p_i(t)\), \(\gamma_{ii}^n(\tau)\), evaluated for a delay \(\tau\). The faster the PLL is, the closer the phase difference is to 0 and the autocorrelation function is closer to its peak value of 1. However, the less coherent the signal is and the shorter is its coherence time, the more erratic is its phase function, and a smaller \(\tau\) will be required to stay close to the autocorrelation peak (see §A.2). For signals that are asymptotically completely incoherent (white noise), the coherence time \(\Delta \tau \ll \tau\), i.e., no \(\tau\) will be short enough to minimize \(\varphi(t_n + \tau) - \varphi(t_n)\), which will assume a different value between time instances \(t_n\) and will average to zero for the entire ensemble. In contrast, for signals that are asymptotically completely coherent along with small \(\tau\) from the PLL, or \(\Delta \tau \gg \tau\), then \(\varphi(t_n + \tau) - \varphi(t_n) \approx \mathop{\mathrm{const}}\)—a constant phase term that may be also taken out of the sum and does not affect the coherence magnitude.

Now, the operation of the PLL is also tied to the third term in Eq. 9.21, which is the instantaneous value of the phase error term \(\varphi_e(t_n + \tau)\). When the PLL is locked to the signal, the phase error is small and fluctuates around 0 (or another constant) \(|\varphi_e(t)| < \epsilon \approx 0\). Once again, this is a constant term that can be taken out of the sum, effectively making the \(\gamma_{io}(t,\tau) \approx \gamma_{ii}(t,\tau)\) a self-coherence (autocorrelation) function of \(p_i(t)\), evaluated at \(\tau\). When the PLL is unlocked—either because it is in the transient lock-acquisition stage, or because the signal cannot be locked to—then \(\varphi_e(t)\) is unbounded and its effect is identical to dealing with an incoherent signal, whose ensemble-average coherence is \(\gamma_{ii}(t,\tau) \ll 1\).

We should remember, though, that both the coherence function and the PLL generally operate in narrowband. If the signal is passed through a bandpass filter in addition to the PLL, then it exaggerates its apparent coherence, which increases with narrower filters (§8.2.8 and §A.2).

In summary, when the PLL receives a coherent input and locks on to it, the output remains coherent, except for the initial transient locking in stage. The output coherence and the input coherence would be asymptotically equal, or

\[ \lim_{\tau,\varphi_e(t) \rightarrow 0} \gamma_{oo} = \gamma_{ii} \]

(9.22)

as long as the finite time of the PLL update speed is virtually instantaneous (\(\tau \rightarrow 0\)) and there are no fluctuations in the phase error (\(\varphi_e(t) \rightarrow 0\)). As the PLL cannot lock in to an incoherent input, its output will remain incoherent over time (subject to the cohering properties of the channel filter).

The coherence of partially coherent signals may be conserved as well, but will be generally somewhere in between the two extremes. For example, some PLL designs cannot lock onto fast linear frequency sweeps. In such a case, \(\varphi_e(t)\) may be unbounded, but deterministic. So depending on the specific signal evolution, coherence may be gradually lost, but not altogether absent such that it acquires a completely random phase error.

We also assumed independence of the channel gain, which may not be true in general. If the gain fluctuates rapidly, the coherence \(\gamma_{io}(t,\tau)\) is expected to decrease.

In conclusion, the above reasoning proves that the PLL is able to conserve the coherence of the input signal under some conditions that are not particularly limiting.

9.6 Motivation for an auditory PLL

While phase locking is a well-studied hallmark feature throughout the auditory pathways (but primarily in the auditory nerve and brainstem), it is usually discussed as a de-facto property of the system (e.g., Heil and Peterson, 2015; Verschooten et al., 2019) rather than as an intended result of a mechanism that acquires locking. The author is unaware of any mention in the auditory research literature of a PLL as a module that is integral to the system—at least not at low-level processing. There has been, however, sporadic jargon borrowed from PLL theory in the context of synchronized spontaneous or evoked otoacoustic emissions (e.g., “pulled in” in Wilson and Sutton, 1981; “frequency locking” in Probst et al., 1991; “capture” in Miller et al., 1997).

Given the complexity of the PLL circuit and operation, why should we invest in applying such a model to the auditory system?

Tying phase locking to an actual PLL module is not pursued merely out of academic interest. There are a few strong reasons that make it especially pertinent to identify a PLL in the auditory system:

1. Phase locking entails conservation of coherence of the input stimulus in the receiver. As will turn out later in this work, coherence and the lack thereof inform much of the intuition of what the auditory system does, also in the context of achieving sharp temporal images. Establishing an earlier source of phase locking in the auditory system is critical in understanding how it deals with different types of signals and what kind of responses can be expected.
2. Tying different organs or circuits in the auditory system with the PLL function may help us demystify their function and potential impairments that are associated with them. A stronger version of this argument is that given that the PLL requires a closed feedback loop to work, studying its components in isolation, as though they can function as part of an open-loop circuit, is mistaken. We will see a clear example for this in the loop filter of the putative PLL.
3. Both PLL theory and practice are vast, so they can undoubtedly provide a conceptual framework and added insight in the analysis of various auditory phenomena that may have resisted treatment with other tools. For example, it may apply to the distinction between transient and steady-state effects, along with a distinction between trackable and untrackable signals.

Because the main focus of the present work is to apply imaging theory concepts to hearing, it is mainly the first reason that has motivated the development of this model. It is impossible to meaningfully understand auditory imaging without a notion of coherence. And it is impossible to understand how coherence is conserved or eroded without a basic notion of phase locking, and arguably for that matter, of PLLs.

9.7 Nonlinear synchronization recast as a PLL

In this section, we attempt to connect a few loose ends between the standard accounts of the cochlear nonlinear dynamics and the phase locking in the auditory-nerve. This will be a stepping stone in identifying a PLL module in the auditory system.

9.7.1 Nonlinear oscillators and PLLs

Despite many commonalities, nonlinear synchronization phenomena and PLL design are generally studied independently. This is not entirely surprising, because opposing aspects of these systems are of particular interest in different disciplines. In synchronization processes, they include nonlinear and chaotic phenomena such as the underlying physical mechanisms of phase locking, Hopf bifurcation, instability (through the Lyapunov exponents), limit cycles and attractors, and synchronization dynamics of multiple oscillators. So a recent interest in PLLs from the nonlinear dynamics perspective has been to uncover how various second- and third-order PLL topologies may be susceptible to chaotic dynamics under some conditions (e.g., Endo and Chua, 1988; Chu et al., 1990; Harb and Harb, 2004; Piqueira, 2017). Chaotic dynamics can be invoked with the right choice of parameters, by modulating the input signal just around the pull-in range, which throws the PLL in and out of lock (Endo and Chua, 1988), and have a response that strongly depends on the initial conditions (Chu et al., 1990). Additionally, period doubling and chaos can be observed when a key parameter is set above a certain threshold (Hopf bifurcation) (Harb and Harb, 2004; Piqueira, 2017). In stark contrast, in PLL engineering, instability is carefully studied in order to be avoided like the plague in all applications. A PLL that self-oscillates, or becomes chaotic, is useless as a module within a larger system.

As it turns out, several generic nonlinear systems that contain a free-running (uncontrolled) oscillator that exhibits synchronization to weakly coupled inputs (i.e., through injection locking) may be remodeled as PLLs without loss of function (Couch, 1971; Schmackers and Mathis, 2005). This has been shown in specific cases for the Van der Pol oscillator, whose equations can be brought to the same form as either first- or second-order PLLs. Additionally, there exists a transformation that can map between the PLL and the other nonlinear system phase-space representations (both system types are generally modeled in different phase-space coordinates) (Schmackers and Mathis, 2005).

Therefore, it is perhaps unsurprising to see how the different nonlinear effects that have been observed in OHC models are also found in PLLs—Hopf bifurcations with limit cycle regime, synchronization, phase slips, possible instability, suppression (referred to as oscillation quenching or death in nonlinear dynamics), and dependence on the input level (e.g., Roongthumskul et al., 2013; Hudspeth, 2014; Chakraborty et al., 2016; Roongthumskul et al., 2021; Pikovsky and Kurths, 2001, p. 229). This equivalence enables us to treat the OHC(s) either as a synchronized oscillator or as a PLL, interchangeably. However, as Pikovsky and Kurths (2001, pp. 40–41) commented, it is frequently very difficult to identify the feedback loop in natural systems with synchronization. Therefore, a practical transformation from the physical nonlinear oscillator to a PLL may not be obvious.

9.7.2 Auditory neural phase locking

In the absence of acoustical input to the auditory system, the auditory nerve discharges spontaneously, in a stochastic manner, at rates that correspond to the fiber sensitivity to sound level—low rates correspond to high threshold units, medium rates to medium thresholds, and high rates to low threshold ones (Kiang et al., 1965; Liberman, 1978). In the presence of pure-tone input from the cochlea, spikes become synchronized to the carrier phase, so their overall temporal pattern is no longer random. This phase locking between the pure tone stimulus and its neurally encoded version is a characteristic of the mammalian auditory nerve (Galambos and Davis, 1943; Tasaki, 1954; Kiang et al., 1965; Rose et al., 1967). See Heil and Peterson (2017) for a review of phase locking in the auditory nerve.

Phase locking has a high-frequency cutoff that varies between mammals and other vertebrates. In humans this limit has been often associated with degraded perception of pitch and melody that is observed above 4–5 kHz (Moore, 2019). In all other mammals tested it is lower than in humans (Köppl, 1997; Palmer and Russell, 1986), whereas in the barn owl it is much higher (9–10 kHz) (Sullivan and Konishi, 1984; Köppl, 1997). While a 4–5 kHz phase-locking cutoff in humans is taken as a standard figure, there has been an ongoing controversy regarding its precise value, and more generally, of its significance in hearing, especially given its limited bandwidth (Verschooten et al., 2019).

In the context of auditory phase locking, a distinction is sometimes made between synchronization and entrainment. The former relates to the temporal precision of the spikes, whereas the latter to the number of spikes per stimulus cycle (Rhode and Smith, 1986b; Joris et al., 1994). The two factors are independent dimensions of auditory temporal coding and were shown to be improved by the existence of the refractory period in the auditory nerve (Avissar et al., 2013).

It is also common to refer to “envelope phase locking” or to “envelope synchronization”, but for reasons that will be discussed in §9.9.2, we will avoid the former expression⁸⁵. Envelope synchronization is distinguished from phase locking to the carrier—both of which are observable in different stimulus conditions (Javel, 1980).

Phase locking is also found throughout the central auditory system (Joris et al., 2004). The high-frequency cutoff within the system progressively deteriorates from the auditory nerve through the brainstem, and midbrain, as the temporal coding is replaced with an average rate coding that dominates the spiking patterns in the thalamus and cortex (Joris et al., 2004). For instance, the ventral cochlear nucleus (VCN) is exceptionally precise in coding the temporal fine structure (even more than the auditory nerve) (Rhode and Smith, 1986b). In contrast, cells of the dorsal cochlear nucleus (DCN) show almost no phase locking to the carrier, despite being sharply tuned spectrally (Rhode and Smith, 1986a), but they show enhanced synchronization to the envelope in comparison with the auditory nerve (Kim et al., 1990; Rhode and Greenberg, 1994; Joris et al., 1994).

A variation of the more general kind of synchronization—mode-locking—was also demonstrated in the auditory system. Mode-locking here refers to exact harmonics of modulation-band frequencies, which were detected as multimodal distributions in the interstimulus intervals of the spiking pattern recordings. The detected peaks had approximately integer ratios, which is indicative of harmonicity (Laudanski et al., 2010). Steady-state mode-locking response was demonstrated in the guinea-pig VCN onset and chopper units using sinusoidal AM tones, synthesized vowels, and harmonic complexes. In a more recent study, Lerud et al. (2014) presented a mode-locking model that could account for 68% of the frequency-following response (FFR) data variance of two musical intervals in the brainstem by Lee et al. (2009). The model relies on dynamic nonlinearities in the brainstem, which generate distortion products that can be used for mode-locking between independent channels. Critically, these studies relate a meaning to mode-locking that is different from the one that is used in nonlinear dynamical systems (Fletcher, 1978; see also §3.3.1 and §9.2), which locks several nearly-harmonic modes to a harmonic oscillation. In contrast, in the two studies mentioned, the modes refer to frequencies that are already part of the modulation spectrum within the channel, or to difference tones between channels. The absence of the standard mode-locking effect might be gathered from measurements of mistuned complex tones in the chinchilla's cochlear nucleus, where primary-like units followed the carrier and were not reported to mode-lock to a nearby harmonic (e.g., Sinex, 2008). For further treatment of mode-locked neural synchronization patterns involving sensorimotor cortical areas see Tass et al. (1998).

9.7.3 The origin of auditory phase locking

It has been occasionally acknowledged that neural phase locking may well originate in the inner ear. For example, Rose et al. (1967) wrote: “It seems thus reasonable to assume that events which determine the effectiveness of the cycle take place peripheral to the fiber, possibly in the nerve endings or other structures of the inner ear.” Russell and Sellick (1978) found that the intracellular receptor potential of guinea-pig IHCs consisted of AC and DC components, but that above 4 kHz, the AC component disappeared and the response was dominated by DC. Given that this frequency is also the phase-locking limit, the authors conjectured, in passing, that the phase locking reflects the receptor AC potential of the IHC. In another introduction, Miller et al. (1997) stated that “Both the spread of synchrony and the capture phenomenon reflect nonlinear signal processing by the cochlea, in that they are not predictable from a fiber's tuning properties.” In their modeling of auditory nerve responses, Peterson and Heil (2020) relate the fact that phase locking does not clip as a function of stimulus level to the mechanoelectrical transduction (MET) nonlinear characteristic response of the IHCs, as well as to their additional low-pass filtering property. Phase locking in the vestibular system has been similarly documented and directly related to the hair bundle deflections (Curthoys et al., 2021): “For phase locking of the primary vestibular afferent to occur, the hair bundle of the receptor(s) must be deflected and activated once per cycle...” See also Figure 1B in Felix II et al. (2018).

Several studies suggested that the spontaneous discharges in the auditory nerve depend upon the input from the cochlea. In chinchillas whose IHCs were ototoxically lesioned, the spontaneous rates dropped significantly in affected fibers—something that could be explained in more than one way, including direct damage to the IHCs (Wang et al., 1997). Additionally, the spontaneous rates in the auditory nerves of cats were shown to logarithmically depend on the endocochlear potential in the scala media, which modulated the rate of action potentials from the IHCs (Sewell, 1984). Interestingly, in direct electric stimulation of the auditory nerve, which bypasses the cochlea and the hair cells, the cat's synchronization index to tones remains significant at least up to 8–10 kHz (Dynes and Delgutte, 1992). Indeed, a correspondence between the inner hair cell synchronized intracellular receptor potential and the auditory nerve cells was pointed to in Weiss and Rose (1988). It was suggested that the high-frequency temporal synchrony degradation is a result of a cascade of three low-pass filters between the hair cell receptor and the auditory nerve. See also Rutherford et al. (2021).

These findings suggest that the spontaneous activity in the auditory nerve is driven by the IHC activity, which is itself irregular, in the absence of any acoustic input. However, spontaneous rate decrease was also observed after de-efferentation of the lateral and medial olivocochlear (LOC and MOC) nerves in the cat (Liberman, 1990). While not considered in the original paper, a mechanical effect of the normal OHC spontaneous activity may drive the IHCs, so its absence after the loss of the MOC may have caused the IHCs to move less. A similar idea was explored in a model by Camalet et al. (2000), where it was proposed that the auditory hearing sensitivity was accomplished by keeping the OHC hair bundle near level-dependent self oscillation, which can explain spontaneous motion as well. Therefore, synchronized activity in the auditory nerve represents a coherent motion of the IHC stereocilia, which may depend to some extent on the OHC oscillation, as weak coupling would entail (see §9.2).

An additional review of the effects of OHC impairment and consequent hearing loss on phase locking function is provided in §17.3.3. The results are somewhat inconsistent and are not always easy to interpret, although association between normal OHC function and phase locking has been documented in several studies, including some very recent ones. In the following, we explore the possibility that phase locking in the IHCs and auditory nerve is impacted by the OHCs.

9.8 The organ of Corti as a PLL

The outer hair cells (OHCs) in the organ of Corti have been a long-standing conundrum in hearing science. Because of their concealed nature and high sensitivity to mechanical insults, direct measurements in the live cochlea are impossible using traditional methods. Additionally, modeling of the OHC dynamics using data gathered in other methods is complicated because the OHCs are deeply embedded in the organ of Corti and are coupled to other structures within it—the reticular lamina, the tectorial membrane, the endocochlear fluid (scala media), connections between the stereocilia via tip links and side connectors, and indirectly to the basilar membrane (BM) through Deiters and pillar cells. Thus, the OHC importance has only started to be unraveled in the last four decades using indirect measures—ever since the discovery of otoacoustic emissions by Kemp (1978). Some of the most characteristic features of the mammalian hearing have been associated with the OHCs: the amplification of low-level signals, the nonlinear compression of high-level inputs, the sharpening of the auditory filters, the generation of intermodulation distortion products, and two-tone suppression. The OHCs themselves have several unique biomechanical features that may account for these effects in some configurations, although few if any models are unanimously accepted among specialists (Ashmore et al., 2010).

Despite the slowly accumulating data, there is still a lack of firm association between the organ of Corti and phase locking, which makes the integration of the mechanical and neural auditory segments somewhat conjectural. Nevertheless, we argue in this section that even with the current state of knowledge, the necessary and sufficient components to make a complete PLL circuit are all in place within the organ of Corti and the OHCs, which permits us to treat them as a system.

9.8.1 Identifying the PLL components

A PLL should have at least two elements—a phase detector and an oscillator—and preferably three—including a loop filter between the other two. These elements must be connected with a feedback loop in order to work as a PLL. The forward gain of the entire module may be larger than unity with no loss of generality, as long as it is stable. Below, we attempt to associate these functions with the known physiology of the organ of Corti, and in particular, the OHCs.

The phase detector

A phase detector is a nonlinear device that produces an output that is proportional to the difference between two inputs. In audio it is referred to as intermodulation distortion, which translates to difference tones, in the case of two pure-tone inputs. In general, the nonlinearity also produces summation tones, which should be removed by the low-pass filter. It is well-known that the ear produces combination tones of frequencies \(mf_1 \pm nf_2 >0\), for two closely-spaced pure tones \(f_1\) and \(f_2\) and positive integers \(m\) and \(n\), with notable difference components that are related to cubic distortion (i.e., \(2f_2-f_1\)) (Goldstein, 1967a). These tones are psychoacoustically audible and are associated with distortion-product otoacoustic emission (DPOAE) that is measurable in the ear canal (Kim et al., 1980), which appears to cover the entire audio range, as it has been shown to exist in bats at least up to 95 kHz (Kössl, 1992). The quadratic component \(f_2 \pm f_1\) is present too, but it is less dominant in the DPOAE and BM spectra (outside of the organ of Corti) than in the reticular lamina (inside the organ of Corti) (Ren and He, 2020). Further, it is more dominant than the cubic component at the level of the IC than in the cochlea (Arnold and Burkard, 1998). The essential role of intermodulation distortion (mainly the quadratic component) in hearing was recently proposed by Nuttall et al. (2018), as a processing stage that extracts the amplitude envelope of the signal.

While there are several nonlinearities associated with the ear, most of them do not contribute to its intermodulation distortion (Avan et al., 2013). With high confidence, the source for these distortion products is the transduction process of the OHC hair bundle deflections to ionic current through the MET channels. There are two interdependent causes for this nonlinearity, referred to as gating compliance. First, the elasticity of the hair bundles is asymmetrical with respect to the resting position and, additionally, at small displacement amplitudes its stiffness is not constant (Jaramillo et al., 1993). Second, the potassium ion (K\(^+\)) current is nonlinearly dependent on the deflection amplitude and has a sigmoid-like characteristic transfer function (Avan et al., 2013). These distorting nonlinearities depend on the joint deflection of adjacent stereocilia that is achieved by horizontal connectors. The connectors are positioned within and across rows of stereocilia and they also connect the tallest row to the tectorial membrane⁸⁶. When these connectors are missing, as was the case in a special strain of mutant mice, most distortion products disappear (Verpy et al., 2008). These features ensure that the distortion is prominent also at low levels—something that would be unattainable with a static nonlinearity (Barral and Martin, 2012; supporting information). As the locus of nonlinear behavior is in the hair bundle, the distortion products are considerably stronger in the reticular lamina than in the BM (Ren and He, 2020; He and Ren, 2021).

The \(f_2-f_1\) (quadratic) and \(2f_2-f_1\) (cubic) distortion components have different properties, somewhat depending on where they are measured within the auditory system. Their relative intensity depends on the symmetry of the operating point of the nonlinear MET transfer function, which can be biased with DC current, low-frequency tones, or OHC motility blockers (Frank and Kössl, 1996; Brown et al., 2009). Additionally, the DPOAE level of the quadratic but not cubic distortion products changes over time in response to ipsilateral and contralateral tones and broadband noise, which suggests a modulatory role of the olivocochlear efferent system (Brown, 1988; Kirk and Johnstone, 1993; but see Kujawa et al., 1995). Furthermore, only the quadratic distortion product significantly interacts with low-frequency amplitude modulation, and its strength and phase are affected by the activation of the contralateral reflex (Abel et al., 2009). Another difference was noted when the distortion products were measured using electrodes in the IC of the awake chinchilla—the quadratic component was up to an order of magnitude stronger than the cubic component (Arnold and Burkard, 1998). Also, it was shown to depend only on the difference between the primaries, to have a low-pass response for small difference products (\(f_2-f_1 < 100\) Hz), and to monotonically increase with level.

It can be concluded that the hair bundle produces the required distortion that can make the necessary output of a phase detector. However, most studies tested the case where two or more external inputs produced a measurable distortion either in the reticular lamina or the basilar membrane. In the context of a PLL, one of the inputs should be the internal oscillator signal. This may be difficult to measure with steady-state pure-tone measurements that are likely to cause the PLL to lock almost instantly, which entails a negligible or DC phase error signal—the very output that is expected from a phase detector.

The loop filter

The role of the loop filter of the PLL is to set the dynamics of the feedback loop, in addition to the removal of high-frequency components from the output of the phase detector. While the filter is not essential for the operation of a (first-order) PLL, an unfiltered design is rather limited in function and not used much in practice.

If we consider the MET channels of the hair bundle to be the “epicenter” of the phase detector, it is natural to look for a filter within the soma of the OHC, where the ionic current flows, as a function of the hair bundle deflection. In fact, the low-pass response of the cell membrane has been a notorious stumbling block in cochlear amplification modeling—the so-called “RC time constant problem”, which is caused by the low-pass characteristics (resistance-capacitance, RC) of the receptor potential of the cell membrane (Ashmore, 1987; Housley and Ashmore, 1992; Santos-Sacchi, 1992). The low-pass filter characteristic is consistently found in vitro (see Santos-Sacchi et al., 2019 for a summary of relevant studies) and was recently shown to be the case in vivo as well (in gerbils), with cutoff frequencies lower than 3 kHz for basal and lower for apical CFs (Vavakou et al., 2019). Even in apical channels, the cutoff frequency is well below the characteristic frequency (CF) (Vavakou et al., 2019; Figure 4D). In contrast, in a more recent in-vivo study in mice, the low-pass filtering effect was confirmed, but appeared relatively small and insufficient to counter the high-frequency cycle-by-cycle amplification generated by somatic motility, as measured in the organ of Corti (most strongly in the displacement of the tectorial membrane; Dewey et al., 2021). Moreover, its effect in the guinea-pig OHCs in vitro did not produce significant reduction in amplification up to 80 kHz (Santos-Sacchi et al., 2023).

This filter was studied in the context of cochlear amplification, as it may be seen as a hindrance in several cochlear amplifier models, since it prevents them from using high-frequency somatic motility in a straightforward manner as can be observed in vitro (Frank et al., 1999; Ashmore, 2008; Santos-Sacchi, 2019). Without high-frequency response, it is unlikely that the electromotile force can be efficiently used in cochlear amplification over a broad frequency range. Models often try to explain this low-pass filtering away by including alternative electrical pathways, such as extracellular potential or endolymphatic ionic currents in the OHCs (e.g., Dallos and Evans, 1995; Johnson et al., 2011), which also received some support in recent in-vivo measurements in mutant mice (Levic et al., 2022). An alternative solution to the low-pass problem was recently proposed by Rabbitt (2020), who showed that, because of various nonlinear effects, the membrane capacitance of the OHCs is both highly nonlinear and complex. These properties were shown, in vitro, to account for both the low-pass behavior and the full-bandwidth, which is thought to be responding to the stimulus on a cycle-by-cycle basis, as in Frank et al. (1999). Another alternative analysis by Iwasa (2017) suggested that under some mechanical load conditions, effective negative capacitance can mitigate some of the low-pass characteristics of the membrane. Finally, a simpler analysis using a linearized analog circuit model of the OHC amplifier convincingly argued that given the known estimates of the RC filter values, it poses no serious problem of amplification at high frequencies, as it still produces the correct OHC elongation that is known to be required for adequate gain (Altoè and Shera, 2023). At present, one available in-vivo study suggests that the filter does have a detrimental effect on high-frequency amplification (Vavakou et al., 2019), another study suggests that it does not under some conditions (Dewey et al., 2021), and a third one suggests that different mechanisms may be responsible for the low and high frequency responses, so that the effect of the filter itself is limited (Levic et al., 2022).

In the case of a PLL, the low-pass filter is a desirable feature, since it can serve as the loop filter. Some measurements established low-pass characteristics that were conveniently fitted with a two-pole low-pass filter (Ashmore, 1987), or rearranged as a four-pole low-pass transfer function with all but one pole well above the effective passband (Santos-Sacchi et al., 2019). These would imply, respectively, a second-order PLL with three spurious poles, or an inconvenient fifth-order PLL if all poles count. Either way, the existence of this filter implies that the low-frequency distortion products can be used for the PLL function and may have good tracking capability, but may be relatively susceptible to noise, due to its relatively wide bandwidth.

Note that beneficial roles of the RC filter were argued recently. Altoè and Shera (2023) showed that such a filter can improve the signal-to-noise ratio at the output, in the condition of incoherent noise and coherent signal. Along with model data from Peterson and Heil (2020), it additionally supports the idea that such a filter is beneficial in removing undesirable high-frequency harmonic distortion components.

The local oscillator

The next step is to identify an oscillator embedded in the organ of Corti that can be synchronized with an external stimulus. The oscillator has to have two important features. The first feature is that it should be free-running, so to produce periodic output even in the absence of reference input (i.e., a stimulus). The second feature is that it must be tunable using slow error-correction inputs from the phase detector.

The most obvious candidate for the oscillator resides in the OHCs, which are typically identified as the source that generates the spontaneous otoacoustic emission (SOAE)—a feature of an active component in the system, perhaps an amplifier. Thomas Gold attempted to measure such emissions, yet was unsuccessful, probably due to inadequate measurement technology at the time (Kemp, 2007). Glanville et al. (1971) may have been the first to report auditory sound production from a whole family that had emitted sounds from their ears that were externally audible, interpreted as “objective tinnitus”, whereas Wilson (1980b) recorded “subjective tinnitus” emitted from the ear. SOAE was more formally discovered by Kemp (1979) and confirmed shortly after by Zurek (1981). When it is measurable, the emitted tones vary in level, number of components, and frequency between individuals and animals (Lonsbury-Martin and Martin, 2008). Tests using ototoxic drugs, as well as the absence of SOAE in hearing-impaired people suggest that SOAE must come from the cochlea (Probst et al., 1991). It was phenomenologically shown early on that the SOAE can be the result of active filtering that contains an oscillator and a positive feedback loop, which can also exhibit the typical sharp response and phase locking of the ear (Bialek and Wit, 1984). Various tests localized the source of the oscillations at the OHCs, as contralateral stimuli were shown to affect the frequency and amplitude of the SOAE, likely as a result of the olivocochlear efferent bundle (Mott et al., 1989). The emissions were also shown to stem from a nonlinear amplifying mechanism as reflectance and impedance measurements in the ear canals of people with strong SOAEs showed net gain in the reflected energy compared to the incident energy (Burns et al., 1998)⁸⁷.

Animal data provide some evidence for the specific source of emissions from within the OHCs. In a series of in-vitro experiments on the bullfrog's hair cell, the hair bundle movements were identified as a source of spontaneous action (Martin and Hudspeth, 1999; Martin et al., 2001; Martin et al., 2003). The bullfrog's hair bundles in vitro were also found to synchronize with one another, when they were coupled together with an elastic thread, simulating the otolithic membrane that is homologous to the tectorial membrane (Zhang et al., 2015). The combined power of the synchronized cells could potentially give rise to SOAE, if the same mechanism is at play in the mammalian cochlea, which seems to be the case.

Additionally, the hair bundle in the bobtail skink lizard was identified to be the source of amplification, which is thought to be also the source of SOAE (Manley et al., 2001). This lizard has a unique cochlear anatomy with hair cells lined up on both sides of the auditory papilla—the analog organ of the basilar membrane. In this in-vivo study, electrically evoked OAE (EEOAE)—known in mammals to produce acoustic emissions that can be detected externally (Zheng et al., 2006)—were produced by injecting a low AC electric current to the scala media, which was then acoustically modulated at a lower frequency. A mechanical geometrical argument was invoked to predict whether hair bundle motility or lateral membrane motor movement produce either one of two fundamentally different emission patterns. If the modulation causes radial motion of the hair bundles that lie opposite to one another, it should produce beating due to destructive interference between adjacent bundles. Alternatively, vertical motion due to lateral membrane movement of the hair cells should produce in-phase motion due to constructive interference. The EEOAEs measured at the ear canal showed unmistakable beating, leading to the conclusion that the hair bundle is the source of motility (and hence amplification, according to the authors). A direct comparison to mammalian OHCs is impossible, unfortunately, but Manley (2000) suggested that since all nonlinear effects (including amplification) in mammals are found also in other vertebrates, then the cochlear amplification in the various vertebrates may relate to a common ancestor. This may further suggest that the hair-bundle mechanism for the SOAE has not changed significantly between animals, as long as the connection between the SOAE and amplification is also stable between all species. Nevertheless, a definitive proof for the connection between the hair bundle and SOAE in mammals is still lacking.

The second feature of the PLL oscillator—of responding to slow error signals—is the one that enables control and error correction of the PLL output. In the PLL, the phase detector produces a signal that is proportional to the instantaneous phase difference between the oscillator and the reference. When the PLL is locked in, the phase difference is zero, or more realistically, it fluctuates around zero. If it is out of lock, then the difference is a low-frequency error signal (of the order of the difference between the local and input instantaneous frequencies). Therefore, we would like to find out whether the spontaneous oscillations can be tuned or biased using a low-frequency signal. There are a few studies that suggest that this is indeed the case, based on the original observation that SOAEs can be entrained to external tones—usually for emissions between 1 and 2 kHz (Wilson, 1980a; Wilson and Sutton, 1981). For example, Bian (2008) found that in the presence of low-frequency tones (25–100 Hz) the frequency of prominent SOAE peaks increased, although by a smaller frequency interval than the tones. The effect depends on the tone level as well and is generally nonlinear, as at very high levels it can cause suppression of the SOAE. The effect on the SOAE may be prolonged after the offset of a long-term exposure to the tone (Drexl et al., 2016b). Similarly, low frequency tones also amplitude-modulate the DPOAEs, where the modulation depth is higher for quadratic than for cubic distortion products, despite their lower absolute levels (Drexl et al., 2012). This effect is interpreted as a modulation of the operating point of the MET nonlinear transfer function.

The SOAE response to low-frequency tones can be directly attributed to the unusual response that the OHCs have to infrasound that is orders of magnitude more sensitive than that of the IHCs, which ultimately determines the audio threshold (Hensel et al., 2007; Salt and Hullar, 2010). There are three primary reasons for this peculiar low-frequency response (starting below 1000 Hz and reaching 150 dB attenuation at 1 Hz for the IHC input; Salt and Hullar, 2010; Figure 3B): strong attenuation by the middle ear (6 dB/oct, below 1000 Hz), shunting by the helicotrema (6 dB/oct, below 100 Hz), and the fact that at low frequencies the OHCs respond to displacement, whereas the IHCs respond to velocity changes (6 dB/oct below 500 Hz) (e.g., Dallos et al., 1972; Russell and Sellick, 1983). The strong attenuation of infrasound by the middle ear and helicotrema suggests that external tones have to be very loud in order to cause any discernible changes in local oscillations. However, this may not be the case for low tones produced internally through nonlinear distortion. For example, the same 30 Hz from Drexl et al. (2016a) could have been presented inside the cochlea at 60 dB SPL instead of 120 dB SPL outside of it to obtain the same effect. Presumably, spatially localized low-frequency distortion products can be of much lower level and have a more localized effect if they are generated directly at the level of the reticular lamina. The special propensity of infrasound to elicit auditory synchronization has been recently demonstrated using infrasound tones (8 Hz) at threshold level and above, as can be learned from its frequency-following response (FFR) even in the absence of any audible sound Jurado et al. (2023).

All these effects point to a sensitivity of the OHCs to low-frequency biasing and modulation, which interacts with both the putative oscillator and the phase detector. However, injecting the system with such low-frequency inputs is unlikely to be exactly equivalent to a generation of a similar distortion product (phase error signal) within the organ of Corti in the presence of an external stimulus. Therefore, establishing a phase-correction effect within an auditory PLL is likely to require more delicate experimentation in which the complete loop is in operation. If this system indeed works as a PLL, then it is not far-fetched to hypothesize that it has evolved to isolate against external low-frequency noise as much as possible, in order to eliminate spurious biasing of the PLL feedback loop, as well as to maintain a biologically useful crossover between vestibular and acoustic frequencies (Lewis, 1992).

9.8.2 Putting together the auditory PLL

Now that the three PLL components have been identified, we can put them together to make a full circuit. What was omitted from the account above, though, is the somatic motility of the OHCs, which receives the low-frequency error signal as a voltage input from the phase detector and should move accordingly (Evans and Dallos, 1993). If the somatic motility amplifies the error signal, then it effectively injects additional power to the open-loop path, which can be taken as gain along with the low-pass filtering. This interpretation may be supported by a recent in-vivo measurement of quadratic distortion products in the gerbil, which showed that the maximum vibration amplitude is not sharply tuned and is confined to a relatively small “hotspot” that includes the OHCs and the Deiters' cells (Cooper et al., 2018). If it is accepted that the source of the distortion product is the MET channels, then these findings suggest that the phase error is amplified between the hair bundle and the Deiters' cells—along the OHC soma⁸⁸. The idea that somatic motility amplifies the distortion product may also be deduced from findings by Jia and He (2005), who showed in cochlear preparations of gerbils and prestin-knock-out mice that OHC electromotily is necessary for voltage-induced hair bundle motility at medium or large amplitudes. Only small amplitudes could be supported by direct electrical stimulation of the hair bundle when electromotility was inactive. However, ultra-high-frequency (\(>\) 40 kHz) hearing was nevertheless present in prestin-knock-out mice (Li et al., 2022).

Figure 9.4: The auditory PLL with the three usual components of phase detector, low-pass filter, and oscillator, along with an amplification that probably functions as loop gain. The dashed arrow can function as the passive path for the signal, which goes directly to the IHCs and can be dominant at very low or very high levels, when the PLL does not lock, or when there is damage to the OHCs. Otherwise, the output from the PLL and the OHCs is coupled to the IHCs, most likely through the tectorial membrane. An additional control input was added to the somatic motor due to the olivocochlear efferent bundle to the OHCs, which is discussed in §16.4.2.

The feedback loop of the cochlear PLL may work as follows. The hair bundle moves with spontaneous frequency in the vicinity of the resonance of the BM, which is not necessarily detected in otoacoustic recordings. At the CF resonance, the signal carried with the traveling wave causes shear forces to deflect the OHC hair bundles, which mix with the local spontaneous oscillation. The spontaneous and incoming signals are multiplied as a result of the MET channel nonlinearity, but only the low-frequency products pass through as ionic current into the OHC soma. The current causes respective electromotile contractions and elongations of the soma, which in turn feed the local oscillation of the hair bundle. As the local oscillation becomes synchronized to the external signal, the distortion product gets closer to zero, and the somatic motility becomes minimal. The oscillator itself is coupled to the IHCs (probably through the tectorial membrane; Hakizimana and Fridberger, 2021) which transduce the phase-locked output to neural action potentials. See Figure 9.4 for a corresponding diagram of the PLL. While all the components are found within one OHC, it is fully embedded in the organ of Corti, which provides the right amount of coupling to the BM vibrations, as well as isolation between the different parts of the system—mainly below and above the reticular lamina. Note that the entire system is bandlimited by virtue of the passive cochlear filter.

A positive feedback design in the organ of Corti has been hypothesized many times starting from Gold (1948), but with amplification as its foremost goal (e.g., Kemp, 1980; Davis, 1983; Bialek and Wit, 1984; Kemp, 1986; Patuzzi et al., 1989; Dallos, 1992; Yates et al., 1992; Robles and Ruggero, 2001; Lu et al., 2006; Bell, 2007; Ashmore, 2011; Avan et al., 2013 and Fettiplace in Ashmore et al., 2010). The PLL uses a negative feedback loop, which is nevertheless susceptible to instability because of the gain in the low-pass filter stage and the delay that the loop incurs, which can turn the feedback to positive under some conditions. The feedback loop described above has the same route as the one described in Avan et al. (2013, Figure 4), although with somewhat different details that need not be contradictory. The other feedback mechanisms cited above involve returning energy back to the traveling wave in the BM as part of the loop, sometimes with the explicit requirement for a cycle-by-cycle amplification (e.g. Dallos, 1992), which is yet to be demonstrated in vivo (van der Heijden and Versteegh, 2015b; Ren et al., 2016b; He et al., 2018). Instead, our PLL model makes this particular design requirement obsolete at phase locking frequencies.

9.8.3 Interim discussion

While the above arguments do not constitute a direct empirical proof for the existence of a PLL in the cochlea, they entail a reorganization of known mechanisms of the OHCs that suggests a novel solution to several puzzles. These include the difficulty to establish a valid model for the cochlear amplifier, partly due to the time-constant problem, as well as a clearer delineation of the roles of the hair bundle and somatic electromotility (for the extent of these controversies, see for example the transcripts of discussions in Cooper and Kemp, 2009; pp. 468–482; see also Ashmore et al., 2010). However, the regenerative amplifying nature of the system makes the ear a nonstandard design as far as PLL theory goes. Here we have a set of oscillators that are running at very low levels, may provide more gain than typical PLLs in lock, and possibly retain some inertial oscillations after the input signal terminates. Such a circuit may require a more refined modeling effort if proven correct. Most likely, many of the insights obtained by nonlinear dynamic models that have been applied to the OHCs (Hudspeth, 2014) can be reframed as part of a PLL design, although it is not certain that approaching the problem from its nonlinear dynamics is the simplest approach to the problem.

There are additional hints that suggest that the PLL design is probably incomplete in its own right. For example, the various extracellular and perilymphatic currents may still have roles in auditory signal processing that are not captured in the PLL model, or that provide access for dynamic biasing of some of the PLL parameters. There are additional operating point changes and efferent connections to the OHCs that suggest a complex function (e.g., Fettiplace, 2017). Finally, as is theorized in §11.6, the OHCs produce modulatory changes on the basilar membrane stiffness, which impacts the velocity of the traveling wave that seems to result in a phase modulation (time-lens). These stiffness changes are dependent on the same somatic motility as is thought to be oscillating with the phase detector output, which may not correspond to the modulation required for stiffness modulation through the Deiters cells. Therefore, at present it is not clear how the PLL and time lensing functions coalesce and whether they interact (but see §16.4.2).

Other critical issues about the putative oscillator remain unanswered. Are different oscillators shared between channels? Can every inner hair cell have its own local oscillator? Or are there several dominant oscillators that serve multiple channels in their vicinity? Is there any substantive difference in oscillation capability between apical and basal sites? Is there any function for basal high-frequency circuits where they cannot provide phase locking to the carrier frequencies? Are the multiple OHCs in every row perfectly synchronized?

9.9 Corollaries to the PLL

In this section we return to what has originally motivated us to search for an auditory PLL: the conservation of coherence between the mechanical and neural domains. However, coherence conservation cannot be unconditional and is dependent on the specifics of the PLL operation and its ability to lock in to arbitrary signals. While we do not have quantitative details about the actual operation of the putative PLL, it will be insightful to consider some of its properties that are central to its operation. Definitive answers to many of the questions that are raised through the analysis below will have to wait for careful testing of the theory in the future. Nevertheless, a few attempts will be made to provide qualitative bounds on the PLL behavior that follow from theory and from diverse empirical findings.

9.9.1 What signals can acquire lock?

PLLs require coherent inputs to lock onto signals with deterministic phase. Pure tones are obviously coherent, as are different kinds of modulated pure-tone carriers. In contrast, true random Gaussian noise is incoherent by definition and does not contain any predictable phase structure to lock onto (but see §9.9.2 for some qualifications). Most realistic signals fall somewhere in between—they are partially coherent—so they can be locked onto with some error that corresponds to their incoherent part (e.g., Eq. §8.21).

Synchronization to more complex signals than pure tones has been demonstrated as well. Phase locking in the cat was demonstrated with upward and downward linear FM ramp with slopes of up to 15.7 kHz/s, as long as the instantaneous frequency was within the channel's bandwidth (Sinex and Geisler, 1981). Also, sinusoidally frequency-modulated tones are phase-locked at low carrier frequencies (\(<\)1–2 kHz) and low modulation frequencies in the ventral cochlear nucleus of the guinea pig (Paraouty et al., 2018). Synchronization to synthetic speech vowels has also been demonstrated a few times. For example, in cats, formant components dominated the synchronized response, along with distortion components, as some other frequencies were suppressed (Young and Sachs, 1979). However, the synchronization strength varied significantly across the spectrum and did not necessarily achieve the full strength as pure tones would, maybe because of suppression. The synchronization strength was relatively robust down to a SNR of 9 dB. Additional evidence for the negative effect of noise on auditory nerve (steady-state) phase locking was shown to be stronger with poorer SNR and broader noise bandwidth in squirrel monkeys (Rhode et al., 1978). Similar findings were shown in the tree frog (Narins and Wagner, 1989) and to a lesser degree in the bullfrog (Freedman et al., 1988). Phase noise “cleaning” and high robustness to noise are not uncommon in electronic PLL designs—a feature that makes them appear as sharp narrowband filters.

Lock acquisition is more difficult to establish based on FM psychoacoustic data, which suggest that temporal processing may be effective for very slow modulation rates, but probably not so much for fast rates (§6.4.2). In a study that tested discrimination between different glide shapes that connected two frequencies over a fixed duration (i.e., with different curves of instantaneous frequency), the average performance of listeners was not very sensitive and detection could be explained mainly using a place of excitation model (Thyer and Mahar, 2006). These results, as well as those reviewed in §9.9.5 and the example provided in §15.9.4 may suggest that the auditory system capability to lock onto frequency glides is limited.

9.9.2 Is there any spurious or residual phase locking even if the PLL receives incoherent signals?

Synchronization to an input can take place when it has a well-defined phase function over a narrow frequency band, so that any ambiguity about the resultant output can be avoided. The narrowband constrains the range of instantaneous phase changes that are permitted around the linear phase progression of the center frequency. Thus, the input signal provides some predictability for a PLL that reacts to the input within a fraction of a period without getting out of lock. Broadband noise signals are, by definition, random, which means that their phase is also random and cannot be predicted. Still, even a random carrier may carry low-frequency information in the envelope domain that is slowly varying and nonrandom. In hearing research, synchronization to the envelope is also referred to as “phase locking”, occasionally, which can be confusing, because it fails to imply that different detection processes may be employed to lock to the carrier and to the envelope. Synchronization to the envelope can be achieved using noncoherent detection, without resorting to carrier phase locking, which occurs on a much shorter time scale.

There has been significant research about auditory phase-locking to broadband noise—both continuous and clicks (for an exhaustive bibliography of broadband studies see Heil and Peterson, 2017). At the heart of the studies that tested phase locking to noise is the assumption that stationary noise can reveal the inner workings of the linear and static nonlinear auditory processing, as the effects of any dynamic nonlinearities (e.g., spike generation, refractory period) are relatively minor, or can be circumvented in analysis (de Boer and de Jongh, 1978; Eggermont, 1993). A consistent finding is that the auditory nerve locks onto the characteristic frequency of the channel, on average, which reflects the auditory filter resonance (e.g, Ruggero, 1973; Louage et al., 2004). The main explanation for this apparent contradiction (of locking to noise) is that the phase-locked response to broadband noise is dominated by low-frequency components that represent slow modulations to the characteristic frequency carrier of the auditory channel (e.g., Heil and Peterson, 2017). It can be seen, though, that relatively high frequencies are not tracked and the phase locking better represents the envelope of the filtered signal (e.g., Møller, 1983, Figures 9C-D, 10C-D). The extent to which the channel coheres the random noise can be gathered from measurements that display quantities that are similar to coherence time, such as the cross-correlograms in Møller (1983, Figures 1 and 3) and the “Difcor⁸⁹” half-width in Louage et al. (2004, Figure 7). Typically, both measures are less than 1 ms long and get gradually shorter as the characteristic frequency increases. These values can be compared with simple calculations of bandpass-filtered white noise in Figure §A.1, which produce somewhat longer coherence times, depending on the filter type, order, and center frequency.

In light of the present auditory PLL theory, the underlying assumptions and interpretation of the broadband phase-locking studies are unsatisfactory, for two reasons. First, the assumption that the auditory channel can be modeled using a static nonlinearity is wrong, given an active phase-locking device, be it a PLL or other. A PLL would appear linear in steady-state only, but its transient response is dynamically nonlinear and not static—it depends on the initial conditions of the input and on the previous state of the system (i.e., whether it is already in lock)—it is not memoryless. Furthermore, the transient response to coherent signals is degraded by random noise, which is the very signal that is being tested.

The second reason is that phase locking fundamentally depends on the degree of coherence of the input signal, which is used as reference phase. As the input is initially bandpass-filtered by the passive cochlear mechanics, the input to the PLL is more coherent than the original stimulus. Therefore, even random broadband noise that is completely incoherent at the input can acquire some residual coherence once it goes through a bandpass filter, depending on its bandwidth (Reddy and Kirlin, 1979; Jacobsen and Nielsen, 1987, §A.2 and §8.2.8). This is the general effect we derived of the increased temporal coherence between the output and the input of a bandpass filter, which depends on its bandwidth only. While the auditory channels are relatively sharper at high frequencies than they are at low frequencies (e.g., Glasberg and Moore, 1990; Shera et al., 2002; Figure §11.12, right), they are much narrower at low frequencies in terms of their absolute bandwidth—the primary parameter of coherence time (§8.2.4)—and hence appear to be more coherent. The low-frequency components that are extracted from the spectrum (Heil and Peterson, 2017) exhibit spurious phase structure primarily as a result of the broadband input becoming partially coherent. To properly track broadband noise, a PLL must have instantaneous lock-in time and large hold-in range that can accommodate arbitrary phase modulation within its bandpass—unphysical requirements. Even if spurious low-frequency components in the filtered noise can be captured by the PLL's lock, they tend to vanish quickly in real stochastic noise, so the PLL would get in and out of lock intermittently. We will revisit this topic in the context of the psychoacoustic response to narrowband noise modulation input (§13.4.5).

In conclusion, in experiments that employ noise-only stimuli, the noise serves as an energy source that activates the channel—including any oscillators in its range. The actual phase of the noise is immaterial, except for instantaneous low-frequency phase trajectories that are formed by the cohering passive bandpass filter. In the communication engineering framework, this situation maps to noncoherent detection, as amplitude modulation data can still be extracted from such an input signal without its carrier phase. Broadband synchronization data do not represent true phase locking as is understood to be possible below 4 kHz, but rather it relates to very short-term tracking that is at most of the order of the coherence time of the filtered signal and directly depends on the filter bandwidth. It is therefore not clear whether the PLL module has any role in achieving this slow synchronization.

Despite the reservations about using broadband noise in synchronization measurements, a great deal of information can be gathered from such data, as long as care is taken in interpreting them. Several such studies will be cited throughout the text.

9.9.3 What is the approximate pull-in time?

Phase locking is achieved within a finite duration. Since the knowledge about phase locking is based on discrete neural spike patterns, usually measured in steady-state, it may be difficult to estimate the pull-in time of the PLL, especially since it may co-occur with neural transient phenomena, such as refractoriness and adaptation. Note that we do not distinguish here between the pull-in and the lock-in times, since we miss the necessary details about the PLL architecture to tell them apart. However, the pull-in time is longer than the lock-in time and may be easier to observe in the right conditions.

Auditory nerve adaptation to 300 ms tone bursts in the gerbil was effectively modeled using two frequency-dependent time constants: one that describes the rapid changes after onset and is on the order of 0.5–4 ms, and another short-term time constant that is an order of magnitude longer and characterizes the discharge pattern before the steady-state response (Westerman and Smith, 1984). During rapid adaptation, the spike rate is much higher than in the short and steady-state stages and is sensitive to intensity changes. The time constants decrease with frequency. Rhode and Smith (1985) measured the auditory nerve responses to 25 ms tone pips in cats, which enabled better resolution of the rapid stage of the adaptation that was largely in agreement with the gerbil data. Phase synchronization was not reported quantitatively, but from the peristimulus time histograms, it appears almost instantly with relatively little jitter.

In the chicken, refractoriness has been shown to improve the synchronization and entrainment of 40 ms low-frequency tone bursts in the auditory nerve, whenever the period was larger than the refractory period (Avissar et al., 2013). Additionally, the jitter of single-unit responses to the same tone bursts was about equal during the 10 ms onset and offset duration of the stimulus, which suggests uniform phaselock precision throughout (Avissar et al., 2007). However, the first 2.5 ms of the signal onset (a ramp) was excluded from the analysis, so the full transient effect may have been lost. Finally, measurements of the cat's auditory nerve show decreased synchronization and entrainment during the first 5–8 ms from the onset of the low-frequency stimulus—a duration that can count as part of the adaptation period (Heil and Peterson, 2017; Figures 8A and 8B).

In addition to direct physiological effects, it is plausible that the locking-in stage has perceptual correlates as well. For example, a tone burst sounds like a click without tonality if it is extremely short, below the click-pitch threshold. Doughty and Garner (1947) found that for tone bursts presented at 110 dB SPL this threshold is shorter than 4.5 ms for frequencies above 1000 Hz and decreased slightly up to 8000 Hz (4 ms)⁹⁰. Thresholds were higher for lower levels and frequencies below 1000 Hz. Somewhat longer tonal threshold were found as a function of the number of periods at 60 dB by Mark and Rattay (1990). Shorter thresholds for tonality were uncovered by Mohlin (2011), who used much improved methods to control for loudness and introduced proper attack and decay to the envelopes to avoid extra peaks in the spectrum. While the definition used was not exactly identical to the click-pitch threshold by Doughty and Garner (1947), the just-audible tonality threshold values were as low as 2.6 ms for 8000 Hz bursts and were often below 3 ms for frequencies above 3000 Hz and up to 20–23 ms at 150 Hz. Despite these results, we do not know if the pitch perception corresponds to a locking in period in the periphery, or if it depends on a critical time constant that is more central.

The above evidence may be indirectly indicative of the existence of finite but short PLL lock-in time for tones—on the order of 2.5–10 ms, or longer at low frequencies and levels. This duration overlaps with the rapid adaptation stage, although the exact interplay between it and psychoacoustic correlates has to be further explored.

9.9.4 What is the pull-in (capture) frequency range for a given auditory channel?

In principle, because of the presumable multiplicity of OHC oscillators, the totality of the cochlea may achieve simultaneous phaselock in multiple channels, subject to the effects of suppression. Within a single channel, the input to the PLL is bandlimited by the cochlear filter before any phase locking takes place. When the synchronization of a single auditory-nerve unit is measured as a function of frequency, it overlaps with the range of its tuning curve only for low-frequency CFs, but at high frequencies (above 1 kHz) phase locking diminishes quickly and the response no longer reflects the filter. For example, in the guinea-pig, it was shown that for a fiber with CF of 600 Hz, the synchronization is nearly constant for a range of 200–1000 Hz with no clear peak, while for CFs of 2 and 3.5 kHz, the tuning curves were not predictive of synchronization, which was limited to low frequencies only (Palmer and Russell, 1986; Figure 2). Similarly, in measurements of the chinchilla's auditory nerve of both low and high CFs, apical (average driven rate was maximum at CF = 413 Hz) synchronization strength was nearly independent of frequency at 200–2000 Hz (Temchin and Ruggero, 2010; Figure 6). A more basal measurement (CF = 2477 Hz) revealed a bandpass synchronization response that had a sharp peak below 1000 Hz. For all CFs, maximum synchronization strength as a function of CF was highest below 1000 Hz and then gradually fell to negligible phase locking for fibers with \(\mathop{\mathrm{CF}}>4\) kHz and had somewhat better phase locking for fibers with \(\mathop{\mathrm{CF}}<4\) kHz (Temchin and Ruggero, 2010; Figure 7). The authors concluded that the differences found between apical and basal sites of the chinchilla are suggestive of other mammals as well. Data from the rat suggest that at very high CFs, synchronization in the auditory nerve is negligible also at low frequencies unless they are intense (\(> 60\) dB SPL), although it progressively improves in the ventral cochlear nucleus and trapezoid body of the olivary complex (Paolini et al., 2001).

These results suggest that the bandwidth of the PLLs is relatively broad, as long as the carriers are low frequency. The effect of the cochlear bandpass filter is not apparent in many cases—synchronization bandwidth is broader at low frequencies and is anyway limited to them, while at high frequencies it drops. What cannot be gathered from these and similar measurements is what the cause of the phaselock is: weak synchronized within-channel OHCs that correspond to the IHC and its fiber, or perhaps OHCs of a remote channel that resonate with the tone and are weakly coupled to the channel under test. Either way, the low-frequency range may be suitable for coherent detection of only low-frequency carriers, or perhaps for coherent detection of low amplitude-modulated frequencies across the audible spectrum. This can be justified in light of the findings of amplitude-demodulated baseband frequencies caused by the intermodulation distortion in the organ of Corti, which were identified by Nuttall et al. (2018). Theoretically, the baseband components can be coded by the auditory nerve independently of the carrier, given that the auditory nerve in mammals is not tuned.

A large PLL bandwidth suggests a proportionally large loop gain (which usually goes as the square root of the bandwidth in higher-order PLLs). However, the exact relation depends on the PLL order and on other parameters, so no further statements can be made based on the available data.

9.9.5 What changes in the input signal can pull the PLL out of lock?

Changes in the input reference stimulus are potentially capable of pulling the PLL out of steady-state lock. The higher order the PLL is, the more resilient it is to higher-order abrupt changes in the phase function derivatives. Three types of changes are customarily examined: phase step, frequency step, and frequency ramp. A well-designed PLL should be able to track the changes while in lock if they are within its pull-in range (slow) or hold range (fast). A lower-order PLL may struggle to maintain lock and can accumulate phase error in the process, mainly outside of its hold range.

Phase step

The phase step is the most basic signal available to test the PLL transient response. It was tested using a modified slot pattern in a mechanical siren, which produced a phase step of half a cycle and sounded as an interruption in the tone (Hartridge, 1936). It was explained using the cochlear resonator theory of the time, but without any formal proof or quantitative data to support it. Informal tests by the author confirm that the phase step creates an interruption and in some combinations of short durations and carriers, it sounds like the tone effectively starts afresh and becomes double. However, if the phase step is small (around \(10^\circ\) at 500 Hz and increasing to about \(25^\circ\) at 6000 Hz), it becomes imperceptible. When the duration is very short, it sounds like the tone is superimposed with a harshness at the step, but its tonality is not broken. It can be shown that the spectrum of a phase-stepped tone shows a slight spectral broadening of the spectral line, which may not be sufficient to provide a spectral cue for detection. Audio demos for different combinations of carriers and phase steps can be found in /Section 9.9.5 - Frequency and phase steps/Phase steps/.

An indirect effect of phase step may have caused erratic thresholds in a tonal gap detection test by Shailer and Moore (1987). A 200 ms tone (200, 400, 1000, and 2000 Hz) in notched-noise masker was tested, with the gap duration applied at its middle. The gap threshold as a function of gap duration was monotonic only when the phase of the tone was made to be continuous, so it continued from the same phase as though the signal continued uninterrupted. When the phase started anew or was reversed after the gap, the threshold oscillated until it settled at longer gaps (4–10 ms, with longer times for short frequencies). This response could be only partially explained by the ringing of the filters that decays over a few milliseconds after the sound subsides. However, no combination of time constants was able to fully account for the results, so the authors suggested that the effect could be also related to phase locking that has to settle before and after the gap. This explanation also coincides with the PLL model, where the local oscillator retains its lock, at least for a few milliseconds after the sound has ceased, and requires a finite duration to obtain lock to the new phase, after a phase step.

Frequency step

The second basic test for the PLL transient response is a frequency step, which was explicitly reported only once as well. A frequency step is perceived as a click if larger than a semitone, unless it is compensated with an adequate amplitude change (Neustadt, 1965, abstract only). Once again, an informal listening test by the author, suggested that the effect of the step is to produce a subtler interruption than the phase step, which is less noticeable than a click. A large step (say, 10–20% of the carrier) sounds less harsh than a small step. When the duration of the tone is long enough, then even a small step (e.g., 0.1%) is noticeable. Placing the step in the zero crossing has no perceptible effect. Another interesting effect is the apparent continuity of the pitch change, which for small steps may sound more like a ramp than a discrete step—something that may reflect a transient locking-in duration. Audio demos of different carrier and step combinations are available in /Section 9.9.5 - Frequency and phase steps/Frequency steps/. As in the phase step, the putative PLL seems to track this change well, for the most part, although large steps may not tracked per se, but are taken over by other channels, maybe with their own PLLs, which avoids any click-like change.

Frequency ramp

A single study directly tested phase locking in the cat of upward and downward frequency-modulated ramps—the third basic signal that is commonly considered for the PLL. The authors used the inter-stimulus spike intervals as a proxy for instantaneous frequency and showed that it follows closely the instantaneous period of the ramps, or its subharmonics, for slopes up to 15.7 kHz/s, as long as the corresponding instantaneous frequencies were within the passband (Sinex and Geisler, 1981; Figure 10). Unfortunately, the temporal resolution of the original plots does not allow for close inspection of the phase tracking precision—especially in the largest slope, which occurs over about 30 ms, but appears almost like a vertical line in the plots. In another study that tested the phase locking to sinusoidal FM in ventral cochlear nucleus (VCN) units, no degradation of synchronization was reported as a function of the maximum frequency velocity, which depended on the modulation frequency and index (Paraouty et al., 2018)⁹¹.

In a psychoacoustic pitch matching test in humans, tones that were simultaneously frequency and amplitude modulated (triangular modulation at 6 Hz) did not elicit equal pitch as did pure tones of equal carriers (440–1500 Hz) (Iwamiya et al., 1984). Therefore, the AM and FM interacted and the pitch was either overestimated or underestimated as a function of modulation depth. When either the AM or the FM was switched off, the pitch matching was still imperfect. This suggests that insofar as pitch reflects frequency tracking, then it is not instantaneous in humans at these frequencies.

In a series of psychoacoustic experiments, Demany and colleagues showed how the pitch of slow and wide frequency-modulated sounds is perceived asymmetrically with respect to instantaneous frequency trajectories, as peaks are always perceived more distinctly than troughs (Demany and McAnally, 1994; Demany and Clément, 1995a; Demany and Clément, 1995b; Demany and Clément, 1997). So, for example, musicians perceived fewer notes in a frequency-modulated melody than in a discrete-tone version of the same melody, which had its notes placed in the peaks and troughs of the continuous melody (Demany and McAnally, 1994). In another experiment, it was found that the asymmetry was smaller for a center frequency of 4000 Hz than 250 and 1000 Hz, which suggested that the effect depends on phase locking or on the lack thereof (Demany and Clément, 1995a). While a satisfactory explanation for this effect is lacking, it was hypothesized that the perception of the peaks and troughs relies, at least in part, on memory, which suggest that the effect is retroactive and central in nature (Demany and Clément, 1997). These results may be reinforced by those from d'Alessandro et al. (1998), who tested the perception of the start and end frequencies of synthetic vowel glissandos of different durations and extents. Subjects' judgment could be modeled using a weighted time average, in which the extremities received more weight than intermediate frequencies. In another study that tested the pitch matching between asymmetrical (but periodic) FM patterns and a pure tone, subjects tended to assign a higher or lower pitch than the geometric mean (either 1 or 2 kHz) (Etchemendy et al., 2014). The direction of the difference was determined by where the asymmetry was and its relative degree. Modeling had only a limited success and could produce approximately correct predictions using a weighted average of the instantaneous frequency across several channels.

Other studies focused on the discrimination of the rate of linear frequency ramps and found that subjects were able to match it across different frequency ranges (Divenyi, 2004), as well as to discriminate between different slopes (Pollack, 1968; Nabelek and Hirsh, 1969; Dooley and Moore, 1988). The slope of frequency acceleration could be discriminated as well, although not as well as the frequency velocity (Divenyi, 2004).

A few studies tested the continuity illusion of frequency glides that are interrupted either by silence or a white noise burst, to find out how well listeners match the frequency trajectory before and after the interruption. Depending on the task, this requires the listeners to perform an interpolation of the trajectories they hear before or after, or an extrapolation of the sound before the interruption. Ciocca and Bregman (1987) employed logarithmic frequency glides that were interrupted by a loud white noise burst before it was continued again from a different frequency. It was found that subjects were able to match the initial trajectory of the glide (slope and initial frequency), as though the noise was not there, effectively interpolating the sound, often with a correct starting point and slope, on average. Kluender and Jenison (1992) found that with bark-scale (logarithmic) glides disrupted by white noise, listeners tended to underestimate the required post-noise glide. The steeper the glide was, the larger was the underestimation. This corresponded with the underestimation of linear frequency slopes composed of discrete tonal pulses interrupted by noise that was observed by Pollack (1977). However, his results are difficult to interpret because of the unspecified pulses that elicit constant pitch, ostensibly. Because the PLL should lock also to short tones, the results from these studies may indicate that, at least in part, it is higher-level processes that are responsible for the incorrect matches, rather than to the poor tracking of the PLL. In any case, it is a given that a correct answer in any of these tests is possible only if the listener is able to track the initial glide well enough to be able to have the right frequency end point from which to interpolate/extrapolate. Once this is achieved, higher-level cognitive processing may be involved that performs the actual interpolation or extrapolation. Unfortunately, it makes the interpretation of incorrect results in these studies ambiguous, as they can be attributed either to low-level tracking error or to an incorrect cognitive process.

Conclusion

In summary, both physiological and psychoacoustic data that can be indicative of phaselock retention are currently lacking and do not allow for a definitive verdict, especially with regards to linear frequency ramps. The scant data about phase and frequency steps suggest that the PLL remains locked, despite the audible brief interruption associated with the steps. Data from the cat show a clear lock to linear ramps, but it is unknown how well the ramps were tracked, because of poor display resolution. The various listening tests, which spanned across multiple channels (and perhaps multiple PLLs), suggest that in some cases phase tracking lags and is not achieved in real time. However, there could be alternative interpretations for the data and tasks, which would make this conclusion uncertain.

This incomplete analysis can entail that the human PLL is second-order, which accounts for the poor tracking of frequency ramps. This would match the loop filter response of the OHCs, which according to one model could be first order, yielding a second-order PLL. If frequency-ramp tracking turns out to be robust after all, then a third-order PLL may be a better model. Given that some animals rely much more heavily on chirps, it is curious to know if their loop filter properties are more clearly second-order. This applies mainly to bats, as some bat species compensate for Doppler shifts in motion, which theoretically requires a third-order PLL. In reality, this may be unnecessary, since bats appear to achieve their Doppler compensation noncoherently using combined amplitude modulation synchronization and place information, rather than coherent carrier processing that would require very high frequency phase locking (e.g., Pollak and Park, 1995).

9.9.6 Can the PLL become unstable?

A well-designed PLL should be unconditionally stable in the range of operation. Otherwise, it can oscillate with no relation to the input signal. Therefore, a healthy cochlea should have no issue with PLL stability. However, SOAEs that are uncontrolled, a form of objective tinnitus, may be a result of unstable oscillators and PLLs, but is a relatively small fraction of tinnitus suffers—between 1.1% and 9.05% (95% confidence interval, Penner, 1990). Loss of cochlear function is also often assumed to be involved in subjective tinnitus cases, perhaps where dead regions are implicated (e.g., Henry et al., 2014a). However, the fact that it is not generally accompanied with SOAEs may indicate that the problem is of different nature and has a central cause.

9.9.7 What is the effect of the input level on the PLL response?

It was seen earlier that the PLL loop gain grows with the level of the input signal, which is one of its characteristic nonlinear features. The effect of gain in any PLL order is to increase its bandwidth and therefore its ability to track more variable inputs. However, in second-order PLLs and higher, increasing the gain may cause instability and change the various phase locking parameters (e.g., lock-in time, hold-in range). Therefore, maintaining relatively constant level to the PLL can make its operation more predictable and stable.

Intensity effects in neural phase locking are well-documented, so this is only a brief overview of the main ones. The auditory nerve spiking rate to phase-locked tones increases with intensity below 70 dB SPL in the squirrel monkey, and it remains saturated at higher levels (Rose et al., 1967). However, the synchronization strength itself also peaks at 60 dB SPL, but is nearly saturated already at 35 dB SPL and grows only marginally from there. At high levels there is a slight deterioration in synchronization. Somewhat different values were measured for the cat in terms of the peak intensities of the rate and synchronization functions, although the general trends are the same (Heil and Peterson, 2017; Figure 8G-H). In the chinchilla, synchronization saturates at low levels in low-frequency fibers, whereas in high-frequency fibers synchronization keeps increasing with level, also in terms of its bandwidth (Temchin and Ruggero, 2010; Figure 6). In the guinea pig, it was shown how in high-frequency channels (\(>\) 1 kHz)—where no phase locking is measurable—intensity does not have any effect and synchronization remains poor (Palmer and Russell, 1986).

The effect of increased bandwidth with higher intensity can be predicted from the PLL theoretical point of view, as the PLL bandwidth and transfer general is dependent on the input level (Eq. 9.12). However, the saturation of synchronization with input levels is nonstandard and may be related to other factors in the cochlear PLL design and the compressed dynamic range of the neural signal. There could be a design benefit to maintain a more or less stable input level that achieves a good phase locking, despite input fluctuations. A similar function was hypothesized by Carney (2018) with emphasis on envelope synchronization rather than on phase locking to the temporal fine structure.

9.9.8 Conclusion

The above analysis revealed a few of the main features of the auditory PLL in a qualitative manner, albeit patchy. Thus, any conclusions made here will remain at least somewhat uncertain until the system can be analyzed in a more rigorous manner. Nevertheless, this level of analysis is sufficient for the present work, which requires the PLL function primarily in order to be able to account for coherence conservation between the acoustic signal and its neural representation.

The PLL appears to be second-order—or perhaps third-order allowing for efficient linear FM tracking—with relatively large bandwidth that is also level-dependent but dynamically limited. It has a pull-in time of less than 7–10 ms for most signals and probably much less (1–3 ms) in the case of simple changes (perhaps tapping to the hold-in time instead). Lock is maintained in adverse SNR conditions, but broadband noise itself appears to have some residual coherence that makes it not entirely random, as PLL theory normally assumes. The PLL is limited to low-frequency carriers, which vary between species. In humans, the lock is strongest for carriers below 1 kHz and appears to become negligible at 4–5 kHz.

There are several aspects that make the auditory PLL unusual within standard PLL theory. The main one is that it contains a chain of tuned PLLs that roughly correspond to channels, which are activated simultaneously and are weakly coupled. The individual PLL is also level-limited and amplificative, and its output is neurally and nonuniformly sampled. Furthermore, there is a duality between the mechanical OHC oscillator and the neural spike generator that involves spontaneous discharging and internal synchronization between the OHCs, IHCs, and auditory nerve. Differences between the biological and electronic systems are to be expected, although the fundamental principles and related concepts from the electronic and control PLL theory appear to hold for the biological one as well.

9.10 Further PLLs downstream

This chapter has dealt primarily with the most well-documented kind of phase locking in the auditory system, whose origin was traced to the cochlea, but is normally studied by observing neural spiking patterns. However, the advantages of using a PLL are not limited to high-frequency and low-level auditory processing. As we saw earlier, the PLL can be synchronized to an external signal and dispense with the need for a local clock to process it coherently. Phaselock is also robust against noise and various changes in the signal that are not predictable otherwise, which can make it appear like a narrowband filter. Thus, the possibility that the brain employs neural PLLs (NPLLs) may be attractive in the realization of higher-level synchronization functions.

NPLLs have been hypothesized in different contexts than hearing (Hoppensteadt, 1997; Ahissar, 1998), which were recently extended to hearing as well (Ahissar et al., 2023). Simple NPLL models are based on a VCO neuron model that is embedded in various neuron networks, which are studied with respect to their nonlinear dynamics, amongst other aspects (Hoppensteadt, 1997). In another class of models, it was proposed that NPLLs may be common thalamocortical modules that are instrumental in the transformation between a temporal code to a rate code (Ahissar, 1998; Ahissar and Arieli, 2001). Examples were provided primarily from tactile and visual data, but the principles are general enough to be applied to any modality. The involved frequencies that are synchronized to in rate coding in the NPLL scheme are relatively low compared to those in hearing (smaller than 14 Hz; Ahissar and Arieli, 2001). It is hypothesized the NPLL thalamocortical loops may be concentrated in the non-lemniscal areas of the auditory thalamus, where it can point the auditory cortex to home in on the syllabic onset of, for example, at typical running speech rates (Ahissar et al., 2023). However, auditory encoding shifts to a rate code mainly around the IC, where the maximum frequencies are in the hundreds of Hertz, with only few instances of rate coding documented in the cochlear nucleus for the carrier but not the envelope (Joris et al., 2004). Feedback loops of different sorts are found in the auditory system, given its widespread efferent system. This includes thalamocortical loops that have been hypothesized in the context of tinnitus (Eggermont, 2012; pp. 201–202), or in attention switching between auditory streams (Kondo and Kashino, 2009). Different neural oscillators exist in the subcortex as well (e.g., the chopper cells in the CN and IC), which may hypothetically function as local oscillators with a feedback loop. There is no particular reason why an NPLL cannot be conceived further upstream from the thalamus, where it can be used to improve or maintain phaselock, or synchronize together (bind) different events and control processes.

One hypothetical use of NPLLs is to facilitate synchronization to undetected modulation-band modes, which are not available on the level of the individual cochlear channel and require inputs across channels. Direct physiological evidence for different across-channel integration of coherent information has not been framed with respect to NPLLs, though. Different mechanisms may exist that can achieve coherence or synchronization manipulation. The example of coincidence detection was briefly mentioned in §8.6, as a popular neural model for nonstationary coherence detection between different inputs, mode-locking was mentioned in §9.7.2, and broadband information contribution in processing was suggested by Pressnitzer et al. (2001).

9.11 Detection schemes with and without phase locking

Our discussion has revolved around the function of one major phase-locking site, which we identified as the auditory PLL, whereupon it was briefly considered that additional sites could exist that produce a similar function in the brain. Hence, auditory synchronization phenomena do not stop in the cochlea or in the auditory nerve and can take additional forms that may not be independent of one another: within-channel coherence manipulation, across-channel synchronization, and modulation phase-locking within and across channels. Advantages exist to increasing or decreasing the synchronization in all types of processing, depending on the stimulus and context. Theoretically, such an accommodation in synchronization may be instigated either locally or through top-down control. These ideas will be explored in some depth after we discuss auditory sharpness and blur, which we argue are ultimately determined by the degree of coherence of the stimulus (§15). According to this logic, an increase in synchronization of any kind of object enhances its sharpness over a background that is less coherent, or that became desynchronized through processing (or dysfunction) in what we shall later refer to as auditory accommodation (§16). These functions might be helped by the availability of NPLLs throughout the auditory brain.

How do these additional synchronization manipulations square with the idea that the auditory PLL conserves the input coherence? The PLL and the ensuing neural synchronization endow the system with an initial degree of coherence that closely corresponds to the acoustic input (within some limitations, see §9.5). However, by not maximizing it right at the beginning of the processing chain, the system may be benefiting from an operating point from which it may be simpler to decohere/desynchronize the signal or to further cohere/synchronize it (Figure 9.5). Which way the processing should go then likely depends to some extent on top-down control that can bias the processing in order for the auditory scene analysis to go as desired, within physical limitations. Therefore, the auditory PLL may provide the system with the potential to conserve the coherence, rather than relay a fixed coherence associated with the input. The PLL feeds into several pathways that can be processed as coherence-conserving, coherence-enhancing (sharpening), or decohering (blurring). Some of it is determined by virtue of the input signal itself (e.g., if it is completely coherent or incoherent). As the majority of realistic stimuli are partially coherent, they may benefit from dual processing: coherent and noncoherent.

Figure 9.5: A cartoon illustration of the hypothetical operating point of the coherence in the auditory system. The abscissa designates the degree of coherence of the stimulus. The auditory degree of coherence is designated by the ordinate, which relates to the phase-locked neural signal somewhere in the system after the cochlear PLL. The blue circle on the middle curve marks a hypothetical operating point which may be further cohered (i.e., its synchronization increased and be more than the input degree of coherence) by pushing the curve upwards, or decohered with the absence of phase locking or the addition of phase noise by pushing the curve downwards, as marked with the red diamonds. There may be advantages in both types of processing in different situations.

Acknowledgment of a dual-processing strategy, beyond the traditional duplex pitch (Licklider, 1951b; Licklider, 1959) and binaural models (Rayleigh, 1907b), has begun to emerge in literature. It embraces the distinction between the slow temporal envelope and the temporal fine structure (TFS—an indicator of phase locking to the carrier; see §6.4), rather than choose one over the other. Examples can be found in discussions about the avian brainstem processing (Sullivan and Konishi, 1984; Warchol and Dallos, 1990), in the attempt to associate the TFS and the envelope with the where/what streams (Smith et al., 2002), an extension of dorsal and ventral stream model to the brainstem in (Pickles, 2012), normal speech spectrograms are a combination of both envelope and TFS processing that are about equally balanced—almost irrespective of vocoding (Shamma and Lorenzi, 2013), normal and impaired balance of TFS and envelope processing (Henry and Heinz, 2013; Anderson et al., 2013; Hao et al., 2018; Parida et al., 2021), binding of TFS and envelope responses to binaural stimuli (Luo et al., 2017; Wang et al., 2018), differential processing of AM and FM tones as inferred from inconsistent internal noise levels required in modeling (Attia et al., 2021), and mixed place/time pitch models (de Cheveigné, 2005; Moore, 2013; Oxenham, 2022)⁹². As some studies demonstrated how one of these two processing types prevails using different stimuli and conditions, different models selectively indicated which type of processing (envelope or TFS) is required for a particular task (e.g., speech reception, pitch discrimination, localization, musical listening). We would like to reframe this discussion from a communication standpoint.

As was argued in §5.3.2, being a communication system, the auditory system has to detect, or demodulate, arbitrary signals that were modulated in arbitrary ways at the source. Each of the two general detection types excels in the demodulation of some signal types and not in others. The PLL necessarily belongs to a coherent detection scheme, but as was seen in §9.9, it is not unconditionally effective and can sometimes be out of lock even within the phase-locking limit. This can happen, for instance, with incoherent signals, in transience (while locking), or because the acoustic signal propagates toward the listener and picks up noise and becomes distorted, so its initial degree of coherence changes. In such cases, it is advantageous to have noncoherent detection that is more general and can intercept the signals that for whatever reason cannot be coherently detected. Parallel coherent and noncoherent detection can therefore provide a fail-proof strategy for processing arbitrary sounds in arbitrary conditions. Hypothetically, the doubly-detected product—the demodulated message—can then be optimally weighted and mixed to produce a superior output. Optical images were interpreted as two-dimensional communication in §5.4.1 and as such they can visually provide a demonstration of the difference between coherent and noncoherent detection. Examples are given in Figures §8.3 for a gradation of coherent, partially coherent, and incoherent images, and in Figure 9.6 for extreme differences between incoherent and coherent imaging.

Figure 9.6: Two images of a polished slice of agate rock back-lit by an incoherent LED source (left) and a coherent laser source (right). The laser beam was spread with a diverging lens and a glass diffuser and its center can be observed in the brightest point from behind the agate. More technical details about the sources are in Figure §8.3. These images illustrate how the information about the object can be observed using both types of illumination, which nevertheless produce different effects. The incoherent image is smooth and clear, whereas the coherent image appears grainy, as the light scatters from the various imperfections in its path and in the agate.

Out of the different available experimental methods that have been used to demonstrate envelope or TFS processing in different conditions, the frequency following response (FFR) is probably the only one that can reveal concurrent information of both processing types. The FFR is a brain potential measurement technique, whose response to sustained and transient sounds corresponds to the low-frequency range (typically \(<\) 2 kHz; up to 1.4 kHz phase locked response has been observed by Bidelman and Powers, 2018) of broadband signals at a short latency from the input (Moushegian et al., 1973). The potential is the summation of multiple areas in the brain and is not necessarily well-localized, although the inferior colliculus (IC) has been usually implicated as the strongest source compared to other subcortical and cortical areas (Chandrasekaran and Kraus, 2010; Tichko and Skoe, 2017; Coffey et al., 2019; Bidelman and Momtaz, 2021). The FFR generally relies on synchronization to different parts of the signal that include a mixture of envelope and TFS. It is possible to estimate the phase locking to TFS by repeating the FFR measurement with inverted polarity (in anti-phase) (Aiken and Picton, 2008). Because the auditory nerve codes only half the wave (Brugge et al., 1969), the polarity inversion forces it to code the half-wave that was rejected in the noninverted run. Subtracting the responses of the two runs eliminates the common factor, which is taken to be the slow-varying temporal envelope, so the remainder is then the response to the fast-varying TFS, or \(\mathop{\mathrm{FFR}}_{TFS} = (\mathop{\mathrm{FFR}}_+ - \mathop{\mathrm{FFR}}_-)/2\), where the sum yields the envelope, \(\mathop{\mathrm{FFR}}_{ENV} = (\mathop{\mathrm{FFR}}_+ + \mathop{\mathrm{FFR}}_-)/2\).

It should be emphasized that the relative magnitude of the FFR measurements necessarily depends on the degree of coherence of the signal that is being heard. As was seen in §5.3.1 and throughout the present chapter, processing the carrier phase requires coherent detection, whereas the envelope can be detected both coherently and noncoherently. Therefore, we can roughly consider \(\mathop{\mathrm{FFR}}_{ENV}\) data to be telling of noncoherent detection and \(\mathop{\mathrm{FFR}}_{TFS}\) of coherent detection. Partially coherent signals can always be represented as a weighted sum of the incoherent and coherent parts of the signal (Eq. §8.21), so in principle, this role division can be universally suitable for arbitrary signal coherence. However, this method cannot tell us with confidence that the temporal envelope was not processed by coherent detection mechanisms—only what was certainly not detected noncoherently.

The FFR sensitivity to the degree of coherence is useful in quantifying the effects of broadband noise and reverberation on hearing. As was mentioned in §5.3.1 and §9.3, an effective PLL should be able to provide more robust detection of coherent signals in low broadband noise than noncoherent detection—especially at a poor SNR level. A good illustration of this was shown in normal-hearing chinchillas, where the \(\mathop{\mathrm{FFR}}_{TFS}\) for speech in pink-noise-masker (high-pass filtered at 600 Hz) had discernible low-frequency (\(< 750\) Hz displayed) peaks at 0 and -20 dB SNR, whereas \(\mathop{\mathrm{FFR}}_{ENV}\) hardly had any in that range (Parida and Heinz, 2021; Figures 4–5). Additionally, at 10 dB SNR or less, the \(\mathop{\mathrm{FFR}}_{TFS}\) power was larger than that of the \(\mathop{\mathrm{FFR}}_{ENV}\).

It is also interesting to consider the effect of reverberation that decoheres the signal, so that the direct sound may remain coherent (if it is coherent to begin with), whereas cumulative reflections gradually decohere it. Thus, we would expect to observe effective coherent detection only at the onset of the stimuli, as long as the reverberation time is not too long. In normal-hearing listeners, it was found that the fundamental frequency of a vowel is almost immune to the effects of reverberation, while the power of the formant harmonics decreases with increasing reverberation time (Bidelman and Krishnan, 2010). While these results are based only on the standard envelope FFR (with no polarity inversion), they are consistent with the idea that reverberation decoheres the parts of the signal that are best detected coherently. In contrast, the fundamental pitch can be detected noncoherently and is therefore more robust to decoherence.

As a final note, it should be mentioned that a pitch extraction algorithm has been recently introduced, which is based on a digital PLL-like principle—the Period-Modulated Harmonic Locked Loop (PM-HLL) (Hohmann, 2021). The PM-HLL is based on variable delays that track the period of the signal (narrowband, or broadband with multiple PM-HLL implementations) and does not employ an oscillator per se. It has been shown to be highly efficient and precise in tracking the pitch of complex signals, including frequency sweeps and complex tones. The processing has additionally implemented qunatization and stabilization, as is prescribed by the auditory image model of (Patterson et al., 1992; see §1.4.2). While the algorithm does not attempt to adhere to the auditory physiology, its advantage in accounting for TFS processing has been briefly discussed.

9.12 Conclusion

This chapter introduced an auditory PLL model that tailors aspects of operation of the mechanical cochlea and neural phase locking—two auditory subsystems that are known to work in concert, but are not usually modeled together. Additionally, the model provides a continuous link, if only conceptually, between the stimulus coherence and the degree of synchronization that is found in the auditory nerve and beyond. While it is undoubtedly speculative in spirit, much of the evidence that is required to make such a system work is already in place. A degree of speculation, however, may be inevitable in the analysis of any system that works as a loop. Breaking the loop into individual subcomponents makes little sense in explaining the function of such a system as a whole. If accepted, the PLL model has the potential to explain a range of physiological and psychoacoustical phenomena, as all sound that is transduced has to pass through it.

As part of the entire work presented here, the role of the PLL model is relatively minor, perhaps with the exception of the analysis of likely mechanisms to drive auditory accommodation (§16.4). It has been developed in order to shed light on the continuity of the signal coherence between the external environment and the brain. Certain aspects of temporal imaging depend on the degree of coherence that the signal or the system have. Therefore, without a clear account of how the coherence function propagates up to the level of perception, much of that discussion will stay murky. This has also been the main reason for not delving into quantitative modeling of the auditory PLL, which is undoubtedly necessary in order to provide the full picture about this system. However, with the amount of unknowns and the general difficulty to simulate PLLs (let alone a chain of coupled PLLs), this likely deserves a lengthy treatment in its own right.

Even if the PLL model will be eventually rejected, a PLL-like modeling should still be valuable in providing deterministic answers to the standard parameters that are generally employed to characterize phaselock. Some of these parameters were explored in §9.9, but data to confidently estimate them have been generally lacking.

In the second half of this work, the ideas of separate coherent and incoherent processing will be discussed using an imaging optics theoretical framework, which considers the two types of processing as two extremes that are key in the understanding of partially coherent processing.

Footnotes

83. This should not be confused with the PLL type number, which is determined according to the number of integrators in the design—the oscillator is counted as one, and any additional filter pole at \(\omega=0\) counts as an additional integrator. Therefore, a type 1 PLL contains only one integrator—the oscillator itself.

84. This concept is more relevant in discrete PLLs, which update every clock cycle, but is somewhat more abstract with analog continuous PLLs.

85. Phase locking to a stimulus with a known frequency is typically quantified in either one of two ways, based on spike recordings from a single unit. Most commonly, the synchronization index or synchronization strength is estimated by testing for the regularity of the spike timing, as a function of stimulus phase (Goldberg and Brown, 1969), \(R = \sqrt{\left(\sum\limits_{i}^N\sin \varphi_i\right)^2 + \left(\sum\limits_{i}^N\cos \varphi_i\right)^2}/N\), where the spike phase \(\varphi_i\) is determined by segmenting the recordings to windows corresponding to the period of the stimulus tone. If the spiking is completely randomly distributed, then \(R\) approaches zero (often, 0.1–0.2 is considered completely random). The other method of estimating phase locking is based on the post-stimulus time histograms, which provide a time series of spikes that can disclose possible periodic regularity. The histograms may be Fourier-transformed to obtain estimates of potential non-random spectral components (Joris et al., 2004).

86. This degree of embedding should be seen as the minimum, as likely it is much higher. It is based on the classically established interfacing of the OHC and the tectorial membrane. As was noted in §2.2.3, a recent study in guinea pigs demonstrated that the OHCs are fully embedded in the tectorial membrane in the intact organ of Corti (Hakizimana and Fridberger, 2021).

87. An alternative model to SOAE formation, which has been quite successful in accounting for empirical data, hypothesizes that the cochlea works as a cavity that supports standing waves. The resonant modes of the cavity are determined by irregularities in the geometrical arrangement and mechanical parameters of the OHCs in the organ of Corti (Shera and Guinan Jr, 1999; Shera, 2003). Such a system is able to sustain its modes because it has an amplifying medium with active elements, which give rise to what may appear as local oscillators, but is in fact an emergent global oscillatory behavior with very sharp modes. Even this model, however, accepts that there are active cellular elements that perform the amplification and may function as local oscillators, though they cannot be directly tapped by external measurements. See also a recent review of SOAE oscillator models by Wit and Bell (2024). The present theory is agnostic to the precise external manifestation of the oscillator, although such a global resonance system is somewhat more awkward to integrate in light of some of the empirical data that is brought below to substantiate the PLL model.

88. Note that this is not the interpretation given by Cooper et al. (2018), who did not discuss the actual source of distortion. The authors considered the gradient of the distortion product level to be aligned with the forward sound path, from the basilar membrane to the reticular lamina, instead of a reverse effect that we propose here. However, the reticular lamina response always showed a phase lead relative to the basilar membrane, which supports our interpretation.

89. The Difcor is derived from the shuffled correlogram—itself a variation of cross-correlation that was adopted to spike trains (Joris, 2003). The Difcor is suitable to test synchronization to the temporal fine structure of the signal (Louage et al., 2004).

90. The first such experiments were reported by Mach (1886/1959, pp. 266–268), who found much longer thresholds for pitch (20–30 ms at 128 Hz), using a rather crude method.

91. In the sinusoidal FM of Eq. §6.34, the frequency velocity is zero, but we can replace the sine with a cosine in the phase term to obtain a maximum velocity of \(\Delta \omega\) around the carrier. From Eq. §6.31, \(\Delta \dot{\omega} = \omega_m\Delta\omega\). In Paraouty et al. (2018), the maximum \(f_m\) was 10 Hz, and the maximum \(\Delta\omega=0.32\omega_c\). Taking \(f_c=2000\) Hz, we obtain \(\Delta \dot{f} \approx 1020\) Hz/s.

92. A somewhat different dual-processing strategy was proposed more openly by Coffey et al. (2016), regarding the pitch perception of different listeners. Perceived pitch was correlated with frequency-following response (FFR) recordings, which related either to the spectral contents of the stimulus (physical spectrum) or the periodicity pitch, as in the case of the missing fundamental, which requires additional processing. The latter strategy was more dominant among musicians.

References

Abel, Markus, Bergweiler, Steffen, and Gerhard-Multhaupt, R. Synchronization of organ pipes: Experimental observations and modeling. The Journal of the Acoustical Society of America, 119 (4): 2467–2475, 2006.

Abel, Cornelius, Wittekindt, Anna, and Kössl, Manfred. Contralateral acoustic stimulation modulates low-frequency biasing of DPOAE: Efferent influence on cochlear amplifier operating state? Journal of Neurophysiology, 101 (5): 2362–2371, 2009.

Ahissar, Ehud. Temporal-code to rate-code conversion by neuronal phase-locked loops. Neural Computation, 10 (3): 597–650, 1998.

Ahissar, Ehud and Arieli, Amos. Figuring space by time. Neuron, 32 (2): 185–201, 2001.

Ahissar, Ehud, Nelinger, Guy, Assa, Eldad, Karp, Ofer, and Saraf-Sinik, Inbar. Thalamocortical loops as temporal demodulators across senses. Communications Biology, 6 (1): 562, 2023.

Aiken, Steven J and Picton, Terence W. Envelope and spectral frequency-following responses to vowel sounds. Hearing Research, 245 (1-2): 35–47, 2008.

Altoè, Alessandro and Shera, Christopher A. The long outer-hair-cell rc time constant: A feature, not a bug, of the mammalian cochlea. Journal of the Association for Research in Otolaryngology, pages 1–17, 2023.

Anderson, Samira, Parbery-Clark, Alexandra, White-Schwoch, Travis, Drehobl, Sarah, and Kraus, Nina. Effects of hearing loss on the subcortical representation of speech cues. The Journal of the Acoustical Society of America, 133 (5): 3030–3038, 2013.

Appleton, Edward Victor. Automatic synchronization of triode oscillators. In Proceedings of the Cambridge Philosophical Society, volume 21, pages 231–248, 1922.

Arnold, Sally and Burkard, Robert. The auditory evoked potential difference tone and cubic difference tone measured from the inferior colliculus of the chinchilla. The Journal of the Acoustical Society of America, 104 (3): 1565–1573, 1998.

Ashmore, JF. A fast motile response in guinea-pig outer hair cells: The cellular basis of the cochlear amplifier. The Journal of Physiology, 388 (1): 323–347, 1987.

Ashmore, Jonathan. Cochlear outer hair cell motility. Physiological Reviews, 88 (1): 173–210, 2008.

Ashmore, J, Avan, P, Brownell, WE, Dallos, P, Dierkes, K, Fettiplace, R, Grosh, K, Hackney, CM, Hudspeth, AJ, Jülicher, F, Lindner, B, Martin, P, Meaud, J, Petit, C, Santos Sacchi, JR, and Canlon, B. The remarkable cochlear amplifier. Hearing Research, 266 (1): 1–17, 2010.

Ashmore, Jonathan. Pushing the envelope of sound. Neuron, 70 (6): 1021–1022, 2011.

Attia, Sarah, King, Andrew, Varnet, Léo, Ponsot, Emmanuel, and Lorenzi, Christian. Double-pass consistency for amplitude-and frequency-modulation detection in normal-hearing listeners. The Journal of the Acoustical Society of America, 150 (5): 3631–3647, 2021.

Avan, Paul, Büki, Béla, and Petit, Christine. Auditory distortions: Origins and functions. Physiological Reviews, 93 (4): 1563–1619, 2013.

Avissar, Michael, Furman, Adam C, Saunders, James C, and Parsons, Thomas D. Adaptation reduces spike-count reliability, but not spike-timing precision, of auditory nerve responses. Journal of Neuroscience, 27 (24): 6461–6472, 2007.

Avissar, Michael, Wittig, John H, Saunders, James C, and Parsons, Thomas D. Refractoriness enhances temporal coding by auditory nerve fibers. Journal of Neuroscience, 33 (18): 7681–7690, 2013.

Barral, Jérémie and Martin, Pascal. Phantom tones and suppressive masking by active nonlinear oscillation of the hair-cell bundle. Proceedings of the National Academy of Sciences, 109 (21): E1344–E1351, 2012.

Bell, Andrew. Tuning the cochlea: Wave-mediated positive feedback between cells. Biological Cybernetics, 96 (4): 421–438, 2007.

Best, Roland E. Phase-locked loops: Design, simulation, and applications. McGraw-Hill, 5th ed. edition, 2003.

Bialek, William and Wit, Hero P. Quantum limits to oscillator stability: Theory and experiments on acoustic emissions from the human ear. Physics Letters A, 104 (3): 173–178, 1984.

Bian, Lin. Effects of low-frequency biasing on spontaneous otoacoustic emissions: Frequency modulation. The Journal of the Acoustical Society of America, 124 (5): 3009–3021, 2008.

Bidelman, Gavin M and Krishnan, Ananthanarayan. Effects of reverberation on brainstem representation of speech in musicians and non-musicians. Brain Research, 1355: 112–125, 2010.

Bidelman, Gavin and Powers, Louise. Response properties of the human frequency-following response (FFR) to speech and non-speech sounds: Level dependence, adaptation and phase-locking limits. International Journal of Audiology, 57 (9): 665–672, 2018.

Bidelman, Gavin M and Momtaz, Sara. Subcortical rather than cortical sources of the frequency-following response (FFR) relate to speech-in-noise perception in normal-hearing listeners. Neuroscience Letters, 746: 135664, 2021.

Brown, AM. Continuous low level sound alters cochlear mechanics: An efferent effect? Hearing Research, 34 (1): 27–38, 1988.

Brown, Daniel J, Hartsock, Jared J, Gill, Ruth M, Fitzgerald, Hillary E, and Salt, Alec N. Estimating the operating point of the cochlear transducer using low-frequency biased distortion products. The Journal of the Acoustical Society of America, 125 (4): 2129–2145, 2009.

Brugge, John F, Anderson, David J, Hind, Joseph E, and Rose, Jerzy E. Time structure of discharges in single auditory nerve fibers of the squirrel monkey in response to complex periodic sounds. Journal of Neurophysiology, 32 (3): 386–401, 1969.

Burns, Edward M, Keefe, Douglas H, and Ling, Robert. Energy reflectance in the ear canal can exceed unity near spontaneous otoacoustic emission frequencies. The Journal of the Acoustical Society of America, 103 (1): 462–474, 1998.

Camalet, Sébastien, Duke, Thomas, Jülicher, Frank, and Prost, Jacques. Auditory sensitivity provided by self-tuned critical oscillations of hair cells. Proceedings of the National Academy of Sciences, 97 (7): 3183–3188, 2000.

Carney, Laurel H. Supra-threshold hearing and fluctuation profiles: Implications for sensorineural and hidden hearing loss. Journal of the Association for Research in Otolaryngology, pages 1–22, 2018.

Chakraborty, S, Dandapathak, M, and Sarkar, BC. Oscillation quenching in third order phase locked loop coupled by mean field diffusive coupling. Chaos: An Interdisciplinary Journal of Nonlinear Science, 26: 113106, 2016.

Chandrasekaran, Bharath and Kraus, Nina. The scalp-recorded brainstem response to speech: Neural origins and plasticity. Psychophysiology, 47 (2): 236–246, 2010.

de Cheveigné, Alain. Pitch perception models. In Plack, Christopher J, Oxenham, Andrew J, Fay, Richard R., and Popper, Arthur N., editors, Pitch. Springer, 2005.

Chu, Y-H, Chou, J-H, and Chang, SHYANG. Chaos from third-order phase-locked loops with a slowly varying parameter. IEEE Transactions on Circuits and Systems, 37 (9): 1104–1115, 1990.

Ciocca, Valter and Bregman, Albert S. Perceived continuity of gliding and steady-state tones through interrupting noise. Perception & Psychophysics, 42 (5): 476–484, 1987.

Coffey, Emily BJ, Colagrosso, Emilia MG, Lehmann, Alexandre, Schönwiesner, Marc, and Zatorre, Robert J. Individual differences in the frequency-following response: Relation to pitch perception. PloS One, 11 (3): e0152374, 2016.

Coffey, Emily BJ, Nicol, Trent, White-Schwoch, Travis, Chandrasekaran, Bharath, Krizman, Jennifer, Skoe, Erika, Zatorre, Robert J, and Kraus, Nina. Evolving perspectives on the sources of the frequency-following response. Nature Communications, 10 (1): 1–10, 2019.

Cooper, Nigel Paul and Kemp, David T. Concepts and Challenges in the Biophysics of Hearing: Proceedings of the 10th International Workshop on the Mechanics of Hearing, Keele University, Staffordshire, UK, 27-31 July 2008. World Scientific Publishing Co. Pte. Ltd., Danvers, MA, 2009.

Cooper, Nigel P, Vavakou, Anna, and van der Heijden, Marcel. Vibration hotspots reveal longitudinal funneling of sound-evoked motion in the mammalian cochlea. Nature Communications, 9 (1): 1–12, 2018.

Couch II, Leon W. Digital and Analog Communication Systems. Pearson Education Inc., Upper Saddle River, NJ, 8th edition, 2013.

Couch, Leon W. A study of a driven oscillator with fm feedback by use of a phase-lock-loop model. IEEE Transactions on Microwave Theory and Techniques, pages 357–366, 1971.

Curthoys, Ian S, Grant, John Wally, Pastras, Christopher J, Fröhlich, Laura, and Brown, Daniel J. Similarities and differences between vestibular and cochlear systems–A review of clinical and physiological evidence. Frontiers in Neuroscience, page 963, 2021.

Dallos, Peter, Billone, NC, Durrant, JD, Wang, C-Y, and Raynor, S. Cochlear inner and outer hair cells: Functional differences. Science, 177 (4046): 356–358, 1972.

Dallos, Peter. The active cochlea. Journal of Neuroscience, 12 (12): 4575–4585, 1992.

Dallos, Peter and Evans, Burt N. High-frequency motility of outer hair cells and the cochlear amplifier. Science, 267 (5206): 2006–2009, 1995.

Davis, Hallowell. An active process in cochlear mechanics. Hearing Research, 9 (1): 79–90, 1983.

Demany, Laurent and McAnally, Kenneth I. The perception of frequency peaks and troughs in wide frequency modulationsa. The Journal of the Acoustical Society of America, 96 (2): 706–715, 1994.

Demany, Laurent and Clément, Sylvain. The perception of frequency peaks and troughs in wide frequency modulations. II. Effects of frequency register, stimulus uncertainty, and intensity. The Journal of the Acoustical Society of America, 97 (4): 2454–2459, 1995a.

Demany, Laurent and Clément, Sylvain. The perception of frequency peaks and troughs in wide frequency modulations. III. Complex carriers. The Journal of the Acoustical Society of America, 98 (5): 2515–2523, 1995b.

Demany, Laurent and Clément, Sylvain. The perception of frequency peaks and troughs in wide frequency modulations. IV. Effects of modulation waveform. The Journal of the Acoustical Society of America, 102 (5): 2935–2944, 1997.

Dewey, James B, Altoè, Alessandro, Shera, Christopher A, Applegate, Brian E, and Oghalai, John S. Cochlear outer hair cell electromotility enhances organ of Corti motion on a cycle-by-cycle basis at high frequencies in vivo. Proceedings of the National Academy of Sciences, 118 (43), 2021.

Divenyi, Pierre L. Frequency change velocity and acceleration detector: A bird or a red herring? In Pressnitzer, D., de Cheveigné, A., McAdams, S., and Collet, L., editors, Auditory Signal Processing: Physiology, Psychoacoustics, and Models, pages 176–184. Springer-Verlag, 2004.

Dooley, Gary J and Moore, Brian CJ. Duration discrimination of steady and gliding tones: A new method for estimating sensitivity to rate of change. The Journal of the Acoustical Society of America, 84 (4): 1332–1337, 1988.

Doughty, JM and Garner, WR. Pitch characteristics of short tones. I. Two kinds of pitch threshold. Journal of Experimental Psychology, 37 (4): 351, 1947.

Drexl, Markus, Gürkov, Robert, and Krause, Eike. Low-frequency modulated quadratic and cubic distortion product otoacoustic emissions in humans. Hearing Research, 287 (1-2): 91–101, 2012.

Drexl, Markus, Otto, Larissa, Wiegrebe, Lutz, Marquardt, Torsten, Gürkov, Robert, and Krause, Eike. Low-frequency sound exposure causes reversible long-term changes of cochlear transfer characteristics. Hearing Research, 332: 87–94, 2016b.

Drexl, Markus, Krause, Eike, Gürkov, Robert, and Wiegrebe, Lutz. Responses of the human inner ear to low-frequency sound. In van Dijk, Pim, Başkent, Deniz, Gaudrain, Etienne, de Kleine, Emile, Wagner, Anita, and Lanting, Cris, editors, Physiology, Psychoacoustics and Cognition in Normal and Impaired Hearing, pages 275–284. Springer International Publishing AG, Cham, Switzerland, 2016a.

Dynes, Scott BC and Delgutte, Bertrand. Phase-locking of auditory-nerve discharges to sinusoidal electric stimulation of the cochlea. Hearing Research, 58 (1): 79–90, 1992.

Eccles, W. H. and Vincent, J. H. On the variations of wave-length of the oscillations generated by three-electrode thermionic tubes due to changes in filament current, plate voltage, grid voltage, or coupling. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 96 (680): 455–465, 1920.

Eggermont, Jos J. Wiener and volterra analyses applied to the auditory system. Hearing Research, 66 (2): 177–201, 1993.

Eggermont, Jos J. The Neuroscience of Tinnitus. Oxford University Press, Oxford, United Kingdom, 2012.

Endo, Tetsuro and Chua, Leon O. Chaos from phase-locked loops. IEEE Transactions on Circuits and Systems, 35 (8): 987–1003, 1988.

Etchemendy, Pablo E, Eguia, Manuel C, and Mesz, Bruno. Principal pitch of frequency-modulated tones with asymmetrical modulation waveform: A comparison of models. The Journal of the Acoustical Society of America, 135 (3): 1344–1355, 2014.

Evans, Burt N and Dallos, Peter. Stereocilia displacement induced somatic motility of cochlear outer hair cells. Proceedings of the National Academy of Sciences, 90 (18): 8347–8351, 1993.

Felix II, Richard A, Gourévitch, Boris, and Portfors, Christine V. Subcortical pathways: Towards a better understanding of auditory disorders. Hearing Research, 362: 48–60, 2018.

Fettiplace, Robert. Hair cell transduction, tuning, and synaptic transmission in the mammalian cochlea. Comprehensive Physiology, 7 (4): 1197–1227, 2017.

Fletcher, Neville H. Mode locking in nonlinearly excited inharmonic musical oscillators. The Journal of the Acoustical Society of America, 64 (6): 1566–1569, 1978.

Fletcher, Neville H and Rossing, Thomas D. The physics of musical instruments. Springer Science+Business Media New York, 2nd edition, 1998.

Frank, Gerhard and Kössl, Manfred. The acoustic two-tone distortions 2f1-f2 and f2-f1 and their possible relation to changes in the operating point of the cochlear amplifier. Hearing Research, 98 (1-2): 104–115, 1996.

Frank, Gerhard, Hemmert, Werner, and Gummer, Anthony W. Limiting dynamics of high-frequency electromechanical transduction of outer hair cells. Proceedings of the National Academy of Sciences, 96 (8): 4420–4425, 1999.

Freedman, Edward G, Ferragamo, Michael, and Simmons, Andrea Megela. Masking patterns in the bullfrog (Rana anacatesbeiana). II: Physiological effects. The Journal of the Acoustical Society of America, 84 (6): 2081–2091, 1988.

Galambos, Robert and Davis, Hallowell. The response of single auditory-nerve fibers to acoustic stimulation. Journal of Neurophysiology, 6 (1): 39–57, 1943.

Gardner, Floyd M. Phaselock Techniques. John Wiley & Sons, Inc, Hoboken, NJ, 3rd edition, 2005.

Glanville, JD, Coles, RRA, and Sullivan, Brenda M. A family with high-tone objective tinnitus. The Journal of Laryngology & Otology, 85 (1): 1–10, 1971.

Glasberg, Brian R and Moore, Brian CJ. Derivation of auditory filter shapes from notched-noise data. Hearing Research, 47 (1-2): 103–138, 1990.

Gold, Thomas. Hearing. II. The physical basis of the action of the cochlea. Proceedings of the Royal Society of London. Series B-Biological Sciences, 135 (881): 492–498, 1948.

Goldberg, Jay M and Brown, Paul B. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: Some physiological mechanisms of sound localization. Journal of Neurophysiology, 32 (4): 613–636, 1969.

Goldstein, J. L. Auditory nonlinearity. The Journal of the Acoustical Society of America, 41 (3): 676–699, 1967a.

Gripon, M. E. De l'influence qu'exercent sur les vibrations d'une colonne d'air les corps sonores qui l'avoisinent. Annales de chimie et de physique, TB, SER5, T30: 343–390, 1874.

Hakizimana, Pierre and Fridberger, Anders. Inner hair cell stereocilia are embedded in the tectorial membrane. Nature Communications, 12 (1): 1–13, 2021.

Hao, Wenyang, Wang, Qian, Li, Liang, Qiao, Yufei, Gao, Zhiqiang, Ni, Daofeng, and Shang, Yingying. Effects of phase-locking deficits on speech recognition in older adults with presbycusis. Frontiers in Aging Neuroscience, 10: 397, 2018.

Harb, Bassam A and Harb, Ahmad M. Chaos and bifurcation in a third-order phase locked loop. Chaos, Solitons & Fractals, 19 (3): 667–672, 2004.

Hartridge, H. The effect of phase-change on the cochlea. Proceedings of the Physical Society (1926-1948), 48 (1): 145, 1936.

He, Wenxuan, Kemp, David, and Ren, Tianying. Timing of the reticular lamina and basilar membrane vibration in living gerbil cochleae. eLife, 7: e37625, 2018.

He, Wenxuan and Ren, Tianying. The origin of mechanical harmonic distortion within the organ of corti in living gerbil cochleae. Communications Biology, 4 (1): 1–11, 2021.

Heil, Peter and Peterson, Adam J. Basic response properties of auditory nerve fibers: A review. Cell and Tissue Research, 361 (1): 129–158, 2015.

Heil, Peter and Peterson, Adam J. Spike timing in auditory-nerve fibers during spontaneous activity and phase locking. Synapse, 71 (1): 5–36, 2017.

Henry, Kenneth S and Heinz, Michael G. Effects of sensorineural hearing loss on temporal coding of narrowband and broadband signals in the auditory periphery. Hearing Research, 303: 39–47, 2013.

Henry, James A, Roberts, Larry E, Caspary, Donald M, Theodoroff, Sarah M, and Salvi, Richard J. Underlying mechanisms of tinnitus: Review and clinical implications. Journal of the American Academy of Audiology, 25 (1): 5–22, 2014a.

Hensel, Johannes, Scholz, Günther, Hurttig, Ulrike, Mrowinski, Dieter, and Janssen, Thomas. Impact of infrasound on the human cochlea. Hearing Research, 233 (1-2): 67–76, 2007.

Hohmann, Volker. The period-modulated harmonic locked loop (PM-HLL): A low-effort algorithm for rapid time-domain multi-periodicity estimation. Acta Acustica, 5: 56, 2021.

Hoppensteadt, Frank C. An introduction to the mathematics of neurons: Modeling in the frequency domain. Cambridge University Press, Cambridge, United Kingdom, 2nd edition, 1997.

Housley, Gary D and Ashmore, Jonathan F. Ionic currents of outer hair cells isolated from the guinea-pig cochlea. The Journal of Physiology, 448 (1): 73–98, 1992.

Hudspeth, AJ. Integrating the active process of hair cells with cochlear function. Nature Reviews Neuroscience, 15 (9): 600–614, 2014.

Iwamiya, Shin-ichiro, Nishikawa, Shinji, and Kitamura, Otoichi. Perceived principal pitch of fm-am tones when the phase difference between frequency modulation and amplitude modulation is in-phase and anti-phase. Journal of the Acoustical Society of Japan (E), 5 (2): 59–69, 1984.

Iwasa, Kuni H. Negative membrane capacitance of outer hair cells: Electromechanical coupling near resonance. Scientific Reports, 7 (1): 1–8, 2017.

Jacobsen, Finn and Nielsen, TG. Spatial correlation and coherence in a reverberant sound field. Journal of Sound and Vibration, 118 (1): 175–180, 1987.

Jaffe, R and Rechtin, Eberhardt. Design and performance of phase-lock circuits capable of near-optimum performance over a wide range of input signal and noise levels. IRE Transactions on Information Theory, 1 (1): 66–76, 1955.

Jaramillo, F, Markin, VS, and Hudspeth, AJ. Auditory illusions and the single hair cell. Nature, 364 (6437): 527–529, 1993.

Javel, Eric. Coding of am tones in the chinchilla auditory nerve: Implications for the pitch of complex tones. The Journal of the Acoustical Society of America, 68 (1): 133–146, 1980.

Jia, Shuping and He, David ZZ. Motility-associated hair-bundle motion in mammalian outer hair cells. Nature Neuroscience, 8 (8): 1028–1034, 2005.

Johnson, Stuart L, Beurg, Maryline, Marcotti, Walter, and Fettiplace, Robert. Prestin-driven cochlear amplification is not limited by the outer hair cell membrane time constant. Neuron, 70 (6): 1143–1154, 2011.

Joris, Philip X, Carney, Laurel H, Smith, Philip H, and Yin, TC. Enhancement of neural synchronization in the anteroventral cochlear nucleus. I. Responses to tones at the characteristic frequency. Journal of Neurophysiology, 71 (3): 1022–1036, 1994.

Joris, Philip X. Interaural time sensitivity dominated by cochlea-induced envelope patterns. Journal of Neuroscience, 23 (15): 6345–6350, 2003.

Joris, PX, Schreiner, CE, and Rees, A. Neural processing of amplitude-modulated sounds. Physiological Reviews, 84 (2): 541–577, 2004.

Jurado, Carlos, Larrea, Marcelo, Vizuete, Juan, Torres, Mabel, Garzón, Christiam, Rodriguez, Alberto, and Marquardt, Torsten. Infrasound tones at sensation threshold level elicit measurable frequency-following responses. The Journal of the Acoustical Society of America, 154 (1): 50–53, 2023.

Kemp, David T. Stimulated acoustic emissions from within the human auditory system. The Journal of the Acoustical Society of America, 64 (5): 1386–1391, 1978.

Kemp, David T. Evidence of mechanical nonlinearity and frequency selective wave amplification in the cochlea. Archives of oto-rhino-laryngology, 224 (1-2): 37–45, 1979.

Kemp, DT. Towards a model for the origin of cochlear echoes. Hearing Research, 2 (3-4): 533–548, 1980.

Kemp, DT. Otoacoustic emissions, travelling waves and cochlear mechanisms. Hearing Research, 22 (1-3): 95–104, 1986.

Kemp, David T. Otoacoustic emissions: Concepts and origins. In Manley, Geoffrey A, Fay, Richard R, and Popper, Arthur N, editors, Active Processes and Otoacoustic Emissions in Hearing, volume 30, pages 1–38. Springer Science & Business Media, LLC, New York, NY, 2007.

Kiang, Nelson Yuan-Sheng, Watanabe, Takeshi, Thomas, Eleanor C., and Clark, Louise F. Discharge patterns of single fibers in the cat's auditory nerve. In Research Monograph No. 35. The M.I.T. Press, Cambridge, MA, 1965.

Kim, DO, Molnar, CE, and Matthews, JW. Cochlear mechanics: Nonlinear behavior in two-tone responses as reflected in cochlear-nerve-fiber responses and in ear-canal sound pressure. The Journal of the Acoustical Society of America, 67 (5): 1704–1721, 1980.

Kim, DO, Sirianni, JG, and Chang, SO. Responses of DCN-PVCN neurons and auditory nerve fibers in unanesthetized decerebrate cats to AM and pure tones: Analysis with autocorrelation/power-spectrum. Hearing Research, 45 (1-2): 95–113, 1990.

Kirk, DL and Johnstone, BM. Modulation of f2-f1: Evidence for a GABA-ergic efferent system in apical cochlea of the guinea pig. Hearing Research, 67 (1-2): 20–34, 1993.

Kluender, Keith R and Jenison, Rick L. Effects of glide slope, noise intensity, and noise duration on the extrapolation of fm glides through noise. Perception & Psychophysics, 51 (3): 231–238, 1992.

Kondo, Hirohito M and Kashino, Makio. Involvement of the thalamocortical loop in the spontaneous switching of percepts in auditory streaming. Journal of Neuroscience, 29 (40): 12695–12701, 2009.

Köppl, Christine. Phase locking to high frequencies in the auditory nerve and cochlear nucleus magnocellularis of the barn owl, Tyto alba. Journal of Neuroscience, 17 (9): 3312–3321, 1997.

Kössl, Manfred. High frequency distortion products from the ears of two bat species, Megaderma lyra and Carollia perspicillata. Hearing Research, 60 (2): 156–164, 1992.

Kujawa, SG, Fallon, M, and Bobbin, RP. Time-varying alterations in the f2- f1 DPOAE response to continuous primary stimulation I: Response characterization and contribution of the olivocochlear efferents. Hearing Research, 85 (1-2): 142–154, 1995.

Laudanski, Jonathan, Coombes, Stephen, Palmer, Alan R, and Sumner, Christian J. Mode-locked spike trains in responses of ventral cochlear nucleus chopper and onset neurons to periodic stimuli. Journal of Neurophysiology, 103 (3): 1226–1237, 2010.

Lee, Kyung Myun, Skoe, Erika, Kraus, Nina, and Ashley, Richard. Selective subcortical enhancement of musical intervals in musicians. Journal of Neuroscience, 29 (18): 5832–5840, 2009.

Lerud, Karl D, Almonte, Felix V, Kim, Ji Chul, and Large, Edward W. Mode-locking neurodynamics predict human auditory brainstem responses to musical intervals. Hearing Research, 308: 41–49, 2014.

Levic, Snezana, Lukashkina, Victoria A, Simões, Patricio, Lukashkin, Andrei N, and Russell, Ian J. A gap-junction mutation reveals that outer hair cell extracellular receptor potentials drive high-frequency cochlear amplification. Journal of Neuroscience, 42 (42): 7875–7884, 2022.

Lewis, Edwin R. Convergence of design in vertebrate acoustic sensors. In Webster, Douglas B., Fay, Richard R., and Popper, Arthur N., editors, The Evolutionary Biology of Hearing, pages 163–184. Springer-Verlag New York, Inc., 1992.

Li, Jie, Liu, Shuang, Song, Chenmeng, Zhu, Tong, Zhao, Zhikai, Sun, Wenzhi, Wang, Yi, Song, Lei, and Xiong, Wei. Prestin-mediated frequency selectivity does not cover ultrahigh frequencies in mice. Neuroscience Bulletin, 38 (7): 769–784, 2022.

Liberman, M Charles. Auditory-nerve response from cats raised in a low-noise chamber. The Journal of the Acoustical Society of America, 63 (2): 442–455, 1978.

Liberman, M Charles. Effects of chronic cochlear de-efferentation on auditory-nerve response. Hearing Research, 49 (1-3): 209–223, 1990.

Licklider, Joseph Carl Robnett. A duplex theory of pitch perception. Experientia, 7 (4): 128–134, 1951b.

Licklider, Joseph Carl Robnett. Three auditory theories. In Koch, Sigmund, editor, Psychology: A Study of a Science, volume 1, pages 41–144. McGraw-Hill, 1959.

Lonsbury-Martin, Brenda L and Martin, Glen K. Otoacoustic emissions: Basic studies in mammalian models. In Manley, Geoffrey A., Fay, Richard R., and Popper, Arthur N., editors, Active Processes and Otoacoustic Emissions in Hearing, volume 30, pages 261–303. Springer Science+Business Media, LLC, New York, NY, 2008.

Louage, Dries HG, van der Heijden, Marcel, and Joris, Philip X. Temporal properties of responses to broadband noise in the auditory nerve. Journal of Neurophysiology, 91 (5): 2051–2065, 2004.

Lu, Timothy K, Zhak, Serhii, Dallos, Peter, and Sarpeshkar, Rahul. Fast cochlear amplification with slow outer hair cells. Hearing Research, 214 (1-2): 45–67, 2006.

Luo, Lu, Wang, Qian, and Li, Liang. Neural representations of concurrent sounds with overlapping spectra in rat inferior colliculus: Comparisons between temporal-fine structure and envelope. Hearing Research, 353: 87–96, 2017.

Mach, Ernst. The Analysis of Sensations and the Relation of the Physical to the Psychical. Dover Publications, Inc., New York, NY, 1886/1959.

Manley, Geoffrey A. Cochlear mechanisms from a phylogenetic viewpoint. Proceedings of the National Academy of Sciences, 97 (22): 11736–11743, 2000.

Manley, Geoffrey A, Kirk, Des L, Köppl, Christine, and Yates, Graeme K. In vivo evidence for a cochlear amplifier in the hair-cell bundle of lizards. Proceedings of the National Academy of Sciences, 98 (5): 2826–2831, 2001.

Margaris, Nikolaos I. Theory of the Non-Linear Analog Phase Locked Loop. Springer-Verlag Berlin Heidelberg, 2004.

Mark, Hermann E and Rattay, Frank. Frequency discrimination of single-, double-, and triple-cycle sinusoidal acoustic signals. The Journal of the Acoustical Society of America, 88 (1): 560–563, 1990.

Martin, Pascal and Hudspeth, AJ. Active hair-bundle movements can amplify a hair cell's response to oscillatory mechanical stimuli. Proceedings of the National Academy of Sciences, 96 (25): 14306–14311, 1999.

Martin, P, Hudspeth, AJ, and Jülicher, F. Comparison of a hair bundle's spontaneous oscillations with its response to mechanical stimulation reveals the underlying active process. Proceedings of the National Academy of Sciences, 98 (25): 14380–14385, 2001.

Martin, Pascal, Bozovic, D, Choe, Y, and Hudspeth, AJ. Spontaneous oscillation by hair bundles of the bullfrog's sacculus. Journal of Neuroscience, 23 (11): 4533–4548, 2003.

Miller, Roger L, Schilling, John R, Franck, Kevin R, and Young, Eric D. Effects of acoustic trauma on the representation of the vowel /ε/ in cat auditory nerve fibers. The Journal of the Acoustical Society of America, 101 (6): 3602–3616, 1997.

Mohlin, Peter. The just audible tonality of short exponential and gaussian pure tone bursts. The Journal of the Acoustical Society of America, 129 (6): 3827–3836, 2011.

Møller, Aage R. Frequency selectivity of phase-locking of complex sounds in the auditory nerve of the rat. Hearing Research, 11 (3): 267–284, 1983.

Moore, Brian CJ. An introduction to the psychology of hearing. Brill, Leiden, Boston, 6th edition, 2013.

Moore, Brian CJ. The roles of temporal envelope and fine structure information in auditory perception. Acoustical Science and Technology, 40 (2): 61–83, 2019.

Mott, John B, Norton, Susan J, Neely, Stephen T, and Warr, W Bruce. Changes in spontaneous otoacoustic emissions produced by acoustic stimulation of the contralateral ear. Hearing Research, 38 (3): 229–242, 1989.

Moushegian, George, Rupert, Allen L, and Stillman, Robert D. Scalp-recorded early responses in man to frequencies in the speech range. Electroencephalography and Clinical Neurophysiology, 35 (6): 665–667, 1973.

Nabelek, I and Hirsh, IJ. On the discrimination of frequency transitions. The Journal of the Acoustical Society of America, 45 (6): 1510–1519, 1969.

Narins, Peter M and Wagner, Ingeborg. Noise susceptibility and immunity of phase locking in amphibian auditory-nerve fibers. The Journal of the Acoustical Society of America, 85 (3): 1255–1265, 1989.

Neustadt, Herbert M. Click heard when a musical tone makes an abrupt frequency change. The Journal of the Acoustical Society of America, 38 (5): 938–938, 1965.

Nuttall, Alfred L, Ricci, Anthony J, Burwood, George, Harte, James M, Stenfelt, Stefan, Cayé-Thomasen, Per, Ren, Tianying, Ramamoorthy, Sripriya, Zhang, Yuan, Wilson, Teresa, Lunner, Thomas, Moore, Brian C. J., and Fridberger, Anders. A mechanoelectrical mechanism for detection of sound envelopes in the hearing organ. Nature Communications, 9 (1): 1–11, 2018.

Oxenham, Andrew J. Questions and controversies surrounding the perception and neural coding of pitch. Frontiers in Neuroscience, 16: 1074752, 2022.

Palmer, AR and Russell, IJ. Phase-locking in the cochlear nerve of the guinea-pig and its relation to the receptor potential of inner hair-cells. Hearing Research, 24 (1): 1–15, 1986.

Paolini, Antonio G, FitzGerald, John V, Burkitt, Anthony N, and Clark, Graeme M. Temporal processing from the auditory nerve to the medial nucleus of the trapezoid body in the rat. Hearing Research, 159 (1-2): 101–116, 2001.

Paraouty, Nihaad, Stasiak, Arkadiusz, Lorenzi, Christian, Varnet, Léo, and Winter, Ian M. Dual coding of frequency modulation in the ventral cochlear nucleus. Journal of Neuroscience, 38 (17): 4123–4137, 2018.

Parida, Satyabrata and Heinz, Michael G. Noninvasive measures of distorted tonotopic speech coding following noise-induced hearing loss. Journal of the Association for Research in Otolaryngology, 22 (1): 51–66, 2021.

Parida, Satyabrata, Bharadwaj, Hari, and Heinz, Michael G. Spectrally specific temporal analyses of spike-train responses to complex sounds: A unifying framework. PLoS Computational Biology, 17 (2): e1008155, 2021.

Patterson, Roy D, Robinson, K, Holdsworth, J, McKeown, D, Zhang, C, and Allerhand, M. Complex sounds and auditory images. In Cazals, Y., Horner, K., and Demany, L., editors, Auditory Physiology and Perception, volume 83, pages 429–446. Pergamon Press, Oxford, United Kingdom, 1992.

Patuzzi, RB, Yates, GK, and Johnstone, BM. Outer hair cell receptor current and sensorineural hearing loss. Hearing Research, 42 (1): 47–72, 1989.

Penner, MJ. An estimate of the prevalence of tinnitus caused by spontaneous otoacoustic emissions. Archives of Otolaryngology–Head & Neck Surgery, 116 (4): 418–423, 1990.

Peterson, Adam J and Heil, Peter. Phase locking of auditory nerve fibers: the role of lowpass filtering by hair cells. Journal of Neuroscience, 40 (24): 4700–4714, 2020.

Pickles, James O. An Introduction to the Physiology of Hearing. Emerald Group Publishing Limited, Bingley, United Kingdom, 4th edition, 2012.

Arkady aand RosenblumPikovsky, Michael and Kurths, Jürgen. Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge University Press, Cambridge, United Kingdom, 2001.

Piqueira, José Roberto C. Hopf bifurcation and chaos in a third-order phase-locked loop. Communications in Nonlinear Science and Numerical Simulation, 42: 178–186, 2017.

Pollack, Irwin. Detection of rate of change of auditory frequency. Journal of Experimental Psychology, 77 (4): 535, 1968.

Pollack, Irwin. Continuation of auditory frequency gradients across temporal breaks: The auditory poggendorff. Perception & Psychophysics, 21 (6): 563–568, 1977.

Pollak, George D and Park, Thomas J. The inferior colliculus. In Popper, Arthur N. and RichardFay, R., editors, Hearing by Bats, volume 5, pages 296–367. Springer-Verlag New York Inc., New York, NY, 1995.

Pressnitzer, Daniel, Meddis, Ray, Delahaye, Roel, and Winter, Ian M. Physiological correlates of comodulation masking release in the mammalian ventral cochlear nucleus. Journal of Neuroscience, 21 (16): 6377–6386, 2001.

Probst, Rudolf, Lonsbury-Martin, Brenda L, and Martin, Glen K. A review of otoacoustic emissions. The Journal of the Acoustical Society of America, 89 (5): 2027–2067, 1991.

Rabbitt, Richard D. The cochlear outer hair cell speed paradox. Proceedings of the National Academy of Sciences, 117 (36): 21880–21888, 2020.

Rayleigh, Lord. XXVII. Acoustical observations. II. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 7 (42): 149–162, 1879b.

Rayleigh, Lord. XXIV. Acoustical notes.—VII. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 13 (75): 316–333, 1907a.

Rayleigh, Lord. XII. On our perception of sound direction. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 13 (74): 214–232, 1907b.

Rayleigh, John William Strutt. The Theory of Sound. Dover Publications, New York, NY, 2nd edition revised and enlarged edition, 1945. First edition printed 1877.

Reddy, S Narashima and Kirlin, R Lynn. Spectral analysis of auditory evoked potentials with pseudorandom noise excitation. IEEE Transactions on Biomedical Engineering, BME-26 (8): 479–487, 1979.

Ren, Tianying, He, Wenxuan, and Kemp, David. Reticular lamina and basilar membrane vibrations in living mouse cochleae. Proceedings of the National Academy of Sciences, 113 (35): 9910–9915, 2016b.

Ren, Tianying and He, Wenxuan. Two-tone distortion in reticular lamina vibration of the living cochlea. Communications Biology, 3 (1): 1–8, 2020.

Rhode, WS, Geisler, CD, and Kennedy, DT. Auditory nerve fiber response to wide-band noise and tone combinations. Journal of Neurophysiology, 41 (3): 692–704, 1978.

Rhode, William S and Smith, Philip H. Characteristics of tone-pip response patterns in relationship to spontaneous rate in cat auditory nerve fibers. Hearing Research, 18 (2): 159–168, 1985.

Rhode, William S and Smith, Philip H. Physiological studies on neurons in the dorsal cochlear nucleus of cat. Journal of neurophysiology, 56 (2): 287–307, 1986a.

Rhode, William S and Smith, Philip H. Encoding timing and intensity in the ventral cochlear nucleus of the cat. Journal of neurophysiology, 56 (2): 261–286, 1986b.

Rhode, William S and Greenberg, Steven. Encoding of amplitude modulation in the cochlear nucleus of the cat. Journal of Neurophysiology, 71 (5): 1797–1825, 1994.

Robles, Luis and Ruggero, Mario A. Mechanics of the mammalian cochlea. Physiological Reviews, 81 (3): 1305–1352, 2001.

Roongthumskul, Yuttana, Shlomovitz, Roie, Bruinsma, Robijn, and Bozovic, Dolores. Phase slips in oscillatory hair bundles. Physical review letters, 110 (14): 148103, 2013.

Roongthumskul, Yuttana, Faber, Justin, and Bozovic, Dolores. Dynamics of mechanically coupled hair-cell bundles of the inner ear. Biophysical Journal, 120 (2): 205–216, 2021.

Rose, Jerzy E, Brugge, John F, Anderson, David J, and Hind, Joseph E. Phase-locked response to low-frequency tones in single auditory nerve fibers of the squirrel monkey. Journal of Neurophysiology, 30 (4): 769–793, 1967.

Ruggero, Mario A. Response to noise of auditory nerve fibers in the squirrel monkey. Journal of Neurophysiology, 36 (4): 569–587, 1973.

Russell, IJ and Sellick, PM. Intracellular studies of hair cells in the mammalian cochlea. The Journal of Physiology, 284 (1): 261–290, 1978.

Russell, IJ and Sellick, PM. Low-frequency characteristics of intracellularly recorded receptor potentials in guinea-pig cochlear hair cells. The Journal of Physiology, 338 (1): 179–206, 1983.

Rutherford, Mark A, von Gersdorff, Henrique, and Goutman, Juan D. Encoding sound in the cochlea: From receptor potential to afferent discharge. The Journal of Physiology, 599 (10): 2527–2557, 2021.

Salt, Alec N and Hullar, Timothy E. Responses of the ear to low frequency sounds, infrasound and wind turbines. Hearing Research, 268 (1-2): 12–21, 2010.

Santos-Sacchi, J. On the frequency limit and phase of outer hair cell motility: Effects of the membrane filter. Journal of Neuroscience, 12 (5): 1906–1916, 1992.

Santos-Sacchi, Joseph, Iwasa, Kuni H, and Tan, Winston. Outer hair cell electromotility is low-pass filtered relative to the molecular conformational changes that produce nonlinear capacitance. Journal of General Physiology, 151 (12): 1369–1385, 2019.

Santos-Sacchi, J. The speed limit of outer hair cell electromechanical activity. HNO, 67 (3): 159–164, 2019.

Santos-Sacchi, Joseph, Bai, Jun-Ping, and Navaratnam, Dhasakumar. Megahertz sampling of prestin (SLC26a5) voltage-sensor charge movements in outer hair cell membranes reveals ultrasonic activity that may support electromotility and cochlear amplification. Journal of Neuroscience, 43 (14): 2460–2468, 2023.

Schmackers, Judith and Mathis, Wolfgang. Entrainment of driven oscillators and the dynamic behavior of PLL's. In International Symposium on Nonlinear Theory and its Applications (NOLTA2005), Bruges, Belgium, pages 521–524. The Institute of Electronics, Information and Communication Engineers, 2005.

Sewell, William F. The relation between the endocochlear potential and spontaneous activity in auditory nerve fibres of the cat. The Journal of Physiology, 347 (1): 685–696, 1984.

Shailer, Michael J and Moore, Brian CJ. Gap detection and the auditory filter: Phase effects using sinusoidal stimuli. The Journal of the Acoustical Society of America, 81 (4): 1110–1117, 1987.

Shamma, Shihab and Lorenzi, Christian. On the balance of envelope and temporal fine structure in the encoding of speech in the early auditory system. The Journal of the Acoustical Society of America, 133 (5): 2818–2833, 2013.

Shera, Christopher A and Guinan Jr, John J. Evoked otoacoustic emissions arise by two fundamentally different mechanisms: A taxonomy for mammalian oaes. The Journal of the Acoustical Society of America, 105 (2): 782–798, 1999.

Shera, Christopher A, Guinan, John J, and Oxenham, Andrew J. Revised estimates of human cochlear tuning from otoacoustic and behavioral measurements. Proceedings of the National Academy of Sciences, 99 (5): 3318–3323, 2002.

Shera, Christopher A. Mammalian spontaneous otoacoustic emissions are amplitude-stabilized cochlear standing waves. The Journal of the Acoustical Society of America, 114 (1): 244–262, 2003.

Sinex, Donal G and Geisler, C Daniel. Auditory-nerve fiber responses to frequency-modulated tones. Hearing Research, 4 (2): 127–148, 1981.

Sinex, Donal G. Responses of cochlear nucleus neurons to harmonic and mistuned complex tones. Hearing Research, 238 (1-2): 39–48, 2008.

Smith, Zachary M, Delgutte, Bertrand, and Oxenham, Andrew J. Chimaeric sounds reveal dichotomies in auditory perception. Nature, 416 (6876): 87–90, 2002.

Stephens, Donald R. Phase-Locked Loops for Wireless Communications: Digital, Analog and Optical Implementations. Kluwer Academic Publishers, 2nd edition, 2001.

Sullivan, WE and Konishi, M. Segregation of stimulus phase and intensity coding in the cochlear nucleus of the barn owl. Journal of Neuroscience, 4 (7): 1787–1799, 1984.

Tasaki, Ichiji. Nerve impulses in individual auditory nerve fibers of guinea pig. Journal of Neurophysiology, 17 (2): 97–122, 1954.

Tass, P, Rosenblum, MG, Weule, J, Kurths, J, Pikovsky, A, Volkmann, J, Schnitzler, A, and Freund, HJ. Detection of n:m phase locking from noisy data: Application to magnetoencephalography. Physical Review Letters, 81 (15): 3291–3294, 1998.

Temchin, Andrei N and Ruggero, Mario A. Phase-locked responses to tones of chinchilla auditory nerve fibers: Implications for apical cochlear mechanics. Journal of the Association for Research in Otolaryngology, 11 (2): 297–318, 2010.

Thyer, Nick and Mahar, Doug. Discrimination of nonlinear frequency glides. The Journal of the Acoustical Society of America, 119 (5): 2929–2936, 2006.

Tichko, Parker and Skoe, Erika. Frequency-dependent fine structure in the frequency-following response: The byproduct of multiple generators. Hearing Research, 348: 1–15, 2017.

van der Heijden, Marcel and Versteegh, Corstiaen PC. Energy flux in the cochlea: Evidence against power amplification of the traveling wave. Journal of the Association for Research in Otolaryngology, 16 (5): 581–597, 2015b.

van der Pol, Balth. LXXXVIII. On "relaxation-oscillations"�. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 2 (11): 978–992, 1926.

Vavakou, Anna, Cooper, Nigel P, and van der Heijden, Marcel. The frequency limit of outer hair cell motility measured in vivo. eLife, 8: e47667, 2019.

Verpy, Elisabeth, Weil, Dominique, Leibovici, Michel, Goodyear, Richard J, Hamard, Ghislaine, Houdon, Carine, Lefèvre, Gaelle M, Hardelin, Jean-Pierre, Richardson, Guy P, Avan, Paul, and Petit, Christine. Stereocilin-deficient mice reveal the origin of cochlear waveform distortions. Nature, 456 (7219): 255–258, 2008.

Verschooten, Eric, Shamma, Shihab, Oxenham, Andrew J, Moore, Brian CJ, Joris, Philip X, Heinz, Michael G, and Plack, Christopher J. The upper frequency limit for the use of phase locking to code temporal fine structure in humans: A compilation of viewpoints. Hearing Research, 377: 109–121, 2019.

Vincent, J. H. On some experiments in which two neighbouring maintained oscillatory circuits affect a resonating circuit. Proceedings of the Physical Society of London, 32 (1): 84, 1919.

Wang, J, Powers, NL, Hofstetter, P, Trautwein, P, Ding, D, and Salvi, R. Effects of selective inner hair cell loss on auditory nerve fiber threshold, tuning and spontaneous and driven discharge rate. Hearing Research, 107 (1-2): 67–82, 1997.

Wang, Qian, Lu, Hao, Wu, Zhemeng, and Li, Liang. Neural representation of interaural correlation in human auditory brainstem: Comparisons between temporal-fine structure and envelope. Hearing Research, 365: 165–173, 2018.

Warchol, Mark E and Dallos, Peter. Neural coding in the chick cochlear nucleus. Journal of Comparative Physiology A, 166 (5): 721–734, 1990.

Weiss, TF and Rose, C. Stages of degradation of timing information in the cochlea: A comparison of hair-cell and nerve-fiber responses in the alligator lizard. Hearing Research, 33 (2): 167–174, 1988.

Westerman, Larry A and Smith, Robert L. Rapid and short-term adaptation in auditory nerve responses. Hearing Research, 15 (3): 249–260, 1984.

Wilson, JP. Evidence for a cochlear origin for acoustic re-emissions, threshold fine-structure and tonal tinnitus. Hearing Research, 2 (3-4): 233–252, 1980a.

Wilson, JP. Recording of the kemp echo and tinnitus from the ear canal without averaging. Proceedings of the physiological society, 298: 8P–9P, 1980b.

Wilson, JP and Sutton, GJ. Acoustic correlates of tonal tinnitus. In Tinnitus, Ciba Foundation symposium 85, pages 82–107, London, United Kingdom, 1981. Pitman Books Ltd.

Wit, Hero P and Bell, Andrew. Something in our ears is oscillating, but what? A modeller's view of efforts to model spontaneous emissions. Journal of the Association for Research in Otolaryngology, pages 1–16, 2024.

Wolaver, Dan H. Phase-Locked Loop Circuit Design. Prentice Hall, Inc., Englewood, NJ, 1991.

Yates, Graeme K, Johnstone, Brian M, Patuzzi, Robert B, and Robertson, Donald. Mechanical preprocessing in the mammalian cochlea. Trends in Neurosciences, 15 (2): 57–61, 1992.

Young, Eric D and Sachs, Murray B. Representation of steady-state vowels in the temporal aspects of the discharge patterns of populations of auditory-nerve fibers. The Journal of the Acoustical Society of America, 66 (5): 1381–1403, 1979.

Zhang, Tracy-Ying, Ji, Seung, and Bozovic, Dolores. Synchronization of spontaneous active motility of hair cell bundles. PloS one, 10 (11): e0141764, 2015.

Zheng, Jiefu, Zou, Yuan, Ren, Tianying, and Nuttall, Alfred L. An overview of electrically evoked otoacoustic emissions in the mammalian cochlea. Journal of Otology, 1 (1): 45–50, 2006.

Zurek, PM. Spontaneous narrowband acoustic signals emitted by human ears. The Journal of the Acoustical Society of America, 69 (2): 514–523, 1981.

d'Alessandro, Christophe, Rosset, Sophie, and Rossi, Jean-Pierre. The pitch of short-duration fundamental frequency glissandos. The Journal of the Acoustical Society of America, 104 (4): 2339–2348, 1998.

de Boer, E and de Jongh, HR. On cochlear encoding: Potentialities and limitations of the reverse-correlation technique. The Journal of the Acoustical Society of America, 63 (1): 115–135, 1978.
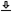