Chapter 6

Physical signals

“In time, I came to the conclusion that the dehydrated cats and the application of Fourier analysis to hearing problems became more and more a handicap for research in hearing.” (Békésy, 1974).

6.1 Introduction

Sound propagation is most generally represented as a wave that is distributed in space and time. But in all common audio applications, it is customary to work with signals rather than waves, which are expressed using a single dimension of time. The spatial dependence is then factored into a frequency-dependent phase and amplitude terms that are fixed as long as the source and receiver are stationary. Mathematically, it simplifies all calculations a great deal. Using the term “signal”, although sometimes synonymous with wave, also confers some intentionality that may be lacking in the normal acoustic wave and implies that it carries information. Typically, signals within the auditory system too are strictly explained in the time domain, which matches the perception of hearing as a temporal sense (§1.3). Nevertheless, we would like to keep sight of the auditory signal and be cognizant that its source is a physical acoustic wave, which may not always be as mathematically idealized as the temporal signal representation implies.

The analytic signal is a powerful signal analytic tool that goes a long way to simplify the treatment of physical signals. It was introduced by Dennis Gabor⁵⁰, when he tried to identify the minimal unit of sound in hearing—the logon—using the uncertainty principle dictated by the Fourier transform (Gabor, 1946). This technique has been widely employed in different fields including hearing research, primarily to decompose signals to their real envelope and temporal fine structure. Unlike the bulk of hearing research, we shall make use of another variation of the analytic signal with a fixed carrier and a complex envelope, which includes all sources of modulation. The complex envelope is commonly used in optics and coherent communication theories, which also provide the theoretical foundation for the present work—in coherence, phase-locked loop, and temporal imaging theories. In these theories, the complex envelope is particularly handy, because it exactly coincides with mathematical solutions to the physical wave problems, which are based on complex amplitudes, or phasors. Therefore, the introduction of the complex envelope will allow us to align the physical solutions in acoustics and optics with the intuition obtained from communication theory regarding modulation.

In this chapter, the analytic signal is derived along with the complex envelope. Emphasis is placed on the narrowband channel condition that is required for the analytic signal to make sense. Then, we take a detour and present an overview of the auditory perception of envelope and phase, or temporal fine structure, as it is commonly referred to. Challenges to the classical and contemporary views are highlighted and a formalism using the complex envelope is contrasted with the standard usage of real envelope. Finally, the status and the implications of the idea that the auditory system performs real demodulation is discussed in light of all of the above, where sound is understood to be best represented by a dual spectrum of carrier and modulation domains.

6.2 The analytic signal

The following overview of the analytic signal compiles a few standard results and draws on derivations from Cohen (1995, pp. 27–43), Mandel and Wolf (1995, pp. 92–102), and Born et al. (2003, pp. 557–562).

We are generally interested in real-valued signals, which are measurable over time regardless of the specific physical system that is being analyzed. Let us consider a time signal \(x(t)\) that has finite energy in the range \(-\infty < t < \infty\), which implies that it is square-integrable

\[ \int_{-\infty}^\infty x^2(t) dt < \infty \]

(6.1)

Thus, the Fourier transform \(X(\omega)\) of this signal exists

\[ X(\omega) = \int_{-\infty}^\infty x(t)e^{-i\omega t} dt \]

(6.2)

where \(\omega = 2\pi f\) is the angular frequency. The inverse Fourier transform is similarly defined as

\[ x(t) = \frac{1}{2\pi}\int_{-\infty}^\infty X(\omega)e^{i\omega t} d\omega \]

(6.3)

Real signals have the convenient property that their Fourier transform is a Hermitian symmetrical function,

\[ X(\omega) = X^*(-\omega) \]

(6.4)

where the \(^*\) is the complex conjugate operation. This property indicates that all the information in \(X(\omega)\) is contained in half the complex plane (including \(\omega = 0\)). Intuitively, positive frequencies are more physically meaningful. As \(X(\omega)\) is generally a complex function, we can redefine the time signal \(x(t)\) as the real part of a complex function \(z(t)\), which is the inverse Fourier transform of the complex function

\[ Z(\omega) = \left\{ \begin{array}{l} X(\omega) \,\,\,\,\,\,\,\, \omega \geq 0\\ 0 \,\,\,\,\,\,\,\,\,\,\,\,\, \omega < 0 \end{array} \right.\ \]

(6.5)

so the spectrum \(Z(\omega)\) is non-zero only for non-negative frequencies, as physical intuition would have. The corresponding time signal is then

\[ z(t) = \frac{1}{2}[x(t) + iy(t)] = \frac{1}{2\pi} \int_{-\infty}^\infty Z(\omega)e^{i\omega t} d\omega = \frac{1}{2\pi} \int_0^\infty Z(\omega)e^{i\omega t} d\omega = \frac{1}{\pi} \int_{0}^\infty X(\omega)e^{i\omega t} d\omega \]

(6.6)

where the last equality used Eq. 6.4 and introduced a factor of 2 to balance the energy of \(z(t)\) and \(x(t)\). We can reintroduce the definition of \(X(\omega)\) from Eq. 6.2 into 6.6

\[ z(t) = \frac{1}{\pi} \int_{0}^\infty \int_{-\infty}^\infty x(t')e^{-i\omega t'} e^{i\omega t} dt' d\omega = \frac{1}{\pi} \int_{0}^\infty \int_{-\infty}^\infty x(t')e^{i\omega (t-t')} dt' d\omega \]

(6.7)

This integral can be solved by using the known transform of the complex exponential⁵¹

\[ \int_{0}^\infty e^{i\omega t} d\omega = \pi \delta(t) + \frac{i}{t} \]

(6.8)

which then yields

\[ z(t) = \frac{1}{\pi} \int_{-\infty}^\infty x(t') \left[\pi \delta(t-t') + \frac{i}{t-t'}\right] dt' d\omega = x(t) + \frac{i}{\pi} \int_{-\infty}^\infty \frac{x(t')}{t-t'} dt' \]

(6.9)

The final integral is the Hilbert transform of \(x(t)\), so

\[ y(t) = {\cal H} [ x(t) ] \equiv \frac{1}{\pi} {\cal P} \int_{-\infty}^\infty \frac{x(t')}{t-t'} dt' \]

(6.10)

in which at \(t' = t\) the integral is evaluated using the Cauchy principal value denoted by \({\cal P}\) (see Mandel and Wolf, 1995; pp. 92–97, for a more rigorous derivation). Similarly, the real part of \(z(t)\) can be obtained from its imaginary part using the inverse Hilbert transform

\[ x(t) = {\cal H}^{-1} [ y(t) ] \equiv -{\cal H} [ y(t) ] = -\frac{1}{\pi} {\cal P} \int_{-\infty}^\infty \frac{y(t')}{t-t'} dt' \]

(6.11)

\(x(t)\) and \(y(t)\) therefore make a Hilbert-transform pair. \(z(t)\) is called the analytic signal of \(x(t)\) and it can be expressed as

\[ z(t) = x(t) + i{\cal H} [ x(t) ] \]

(6.12)

Using this definition, the following equalities follow from Eqs. 6.3 and 6.6, and from Plancharel theorem of the equality of energy in the time and frequency representations of the signal

\[ \int_{-\infty}^\infty x^2(t) dt = \int_{-\infty}^\infty y^2(t) dt = \frac{1}{2}\int_{-\infty}^\infty z(t)z^*(t) dt = \frac{1}{2}\int_{-\infty}^\infty |Z(\omega)|^2d \omega = 2\int_{0}^\infty |X(\omega)|^2d \omega \]

(6.13)

Additionally, the real and imaginary parts of the analytic signal satisfy

\[ \int_{-\infty}^\infty x(t)y(t) dt = 0 \]

(6.14)

This property is used in communication theory to obtain two locally-independent components in the same channel: the real part \(x(t)\) is referred to as the in-phase component and the imaginary part \(y(t)\) is the quadrature-phase component (§5.3.1).

6.3 The narrowband approximation and the complex envelope

The analytic function is most useful for narrowband or quasi-monochromatic signals—different terms that imply that the spectrum is concentrated in a relatively narrow frequency band \(\Delta \omega\) around its center frequency \(\omega_c\)

\[ \frac{\Delta \omega}{\omega_c} \ll 1 \]

(6.15)

Throughout this work, we shall refer to this inequality as the narrowband condition and to its corollaries as resulting from the narrowband approximation. In practice, values as large as \(\Delta \omega / \omega_c \approx 0.2\) may sometime count as narrowband⁵². For these signals it is implied that all the energy is contained in the range

\[ \omega_c - \frac{\Delta \omega}{2} \leq |\omega| \leq \omega_c + \frac{\Delta \omega}{2} \,\,\,\,\,\,\,\,\,\,\,\, \Delta\omega , \omega_c > 0 \]

(6.16)

and outside this range the spectrum is zero, \(X(\omega) = 0\). More relaxed bounds may be implied by the terms bandpass or bandlimited signals, which are not necessarily narrowband. The analytic signal is a complex function and as such, it can be represented in polar form

\[ z(t) = a(t)e^{i\varphi(t)} \]

(6.17)

with \(a(t)\) and \(\varphi(t)\) the amplitude and phase functions, respectively. In the limiting case of a pure tone or strictly monochromatic signal, only a single component exists in the spectrum of \(z(t)\) at \(\omega_c\), as the bandwidth is infinitesimally small, \(\Delta \omega \rightarrow 0\). In this case, \(\varphi(t) = \omega_c t\), \(a(t) = a\) is a complex constant, and the real signal can be written as,

\[ x(t) = 2\Re \left[ z(t) \right] = 2\Re ( a e^{i\omega_c t} ) = a_0 \cos(\omega_c t + \varphi_0) \]

(6.18)

where \(a = \Re \left(\frac{1}{2}a_0 \right)\).

This procedure may be extended for narrowband signals that are quasi-monochromatic, in which both amplitude and phase functions vary in time,

\[ x(t) = a(t) \cos[\omega_c t + \varphi(t)] \]

(6.19)

The choice of \(a(t)\) and \(\varphi(t)\), however, is not unique for \(x(t)\) (Voelcker, 1966). It is made unique by using the corresponding analytic signal definition when \(\omega_c\) is known

\[ z(t) = \frac{1}{2} a(t) e^{i\omega_c t + i\varphi(t)} \]

(6.20)

where both \(a(t)\) and \(\varphi(t)\) are real functions, and \(0 \leq \varphi(t) < 2\pi\). From \(z(t)\), the quadrature component can be readily computed

\[ y(t) = a(t) \sin[\omega_c t + \varphi(t)] \]

(6.21)

(see Figure 6.1). If we dissociate the analytic signal from its linear carrier phase \(\omega_c t\), we obtain

\[ g(t) = a(t) e^{i\varphi(t)} = 2z(t) e^{-i\omega_c t} \]

(6.22)

This expression is referred to as the complex envelope of the real quasi-monochromatic signal \(x(t)\). It is manipulated just like a phasor or a general complex amplitude, which have the same functional forms (Wheeler, 1941). This important concept allows us to examine the envelope independently of the specific carrier frequency, as long as the narrowband approximation holds. The narrowband range of Eq. 6.16 means that with the frequency shift of Eq. 6.22, the complex envelope is non-zero for \(-\Delta \omega \leq \omega \leq \Delta \omega\), which is well-separated from the carrier at \(\omega_c\). This requirement effectively entails that the envelope functions vary much more slowly than the carrier, as \(T \sim 1/\Delta \omega \gg 1/\omega_c \sim T_c\), where \(T\) is the period of the envelope and \(T_c\) is the period of the carrier. When the separation between the envelope and carrier bands is incomplete, the signal is no longer narrowband, and the complex envelope (or any modulation function for that matter) no longer has a useful interpretation, even though the equations still hold (Rihaczek and Bedrosian, 1966).

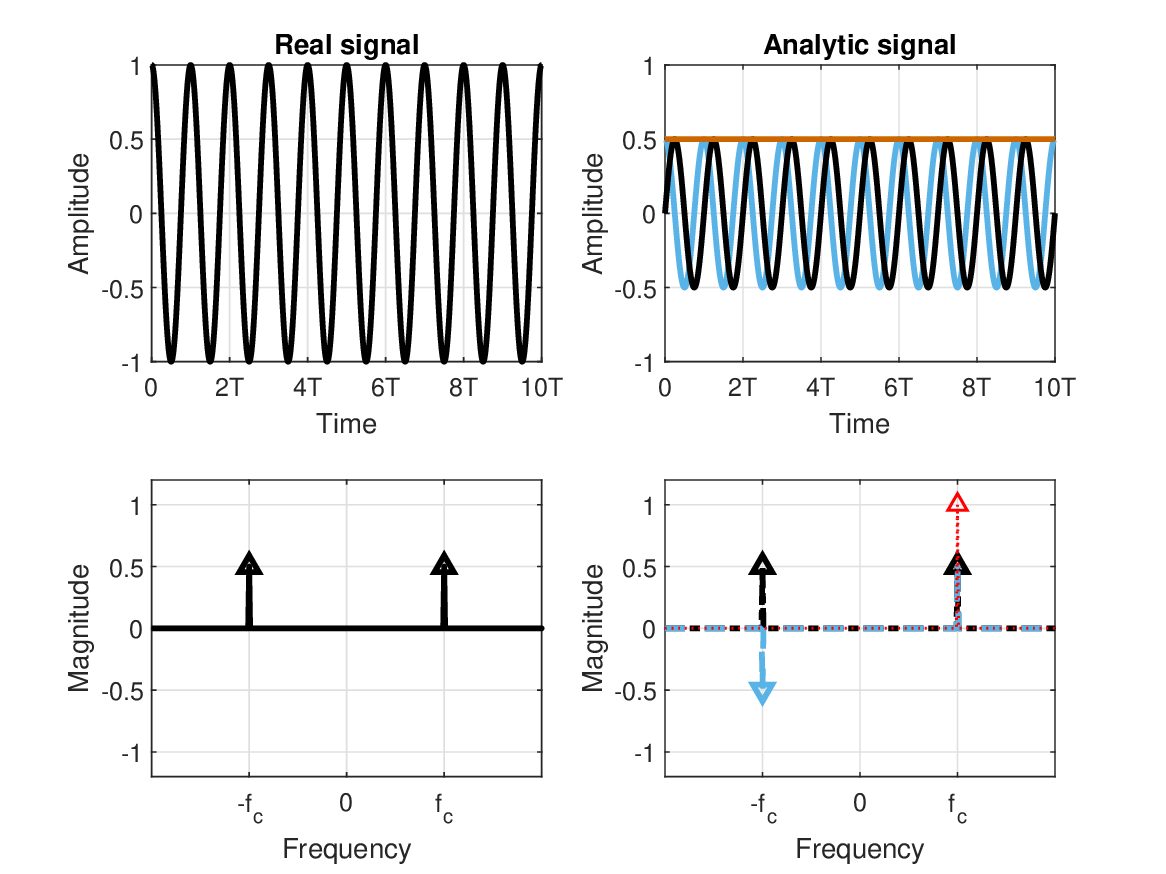
Figure 6.1: The real (standard) time representation of a pure tone / monochromatic signal (top left), its spectrum (bottom left), and their analytic signal counterparts on the right. The real part of the analytic signal is in black and its imaginary part is in blue. On the top right, the constant envelope of the tone is marked in red. On the bottom right, the even and odd components (plotted in black and blue, respectively) are summed to yield the single-sided spectrum component (in red).

In fact, the complex envelope leads to a very general result in communication theory, which shows that any bandpass waveform may be expressed as the real part of the product of the complex envelope and a carrier

\[ x(t) = \Re[g(t)e^{i\omega_c t}] \]

(6.23)

following Eq. 6.22 (we referred to this result as the third canonical signal form in §5.3.1 and Eq. §5.6). It may be drawn directly from the analytic signal definition, and can also be proven relatively straightforwardly in an alternative way, by expanding the bandpass signal \(x(t)\) to its Fourier series (Couch II, 2013; pp. 239–240)

\[ x(t) = \sum_{n = -\infty}^{n=\infty} c_n e^{ i n \omega t} \,\,\,\,\,\,\,\,\,\,\, \omega = \frac{2\pi}{T} \]

(6.24)

For a general non-periodic signal, we examine the series in the limit of \(T \rightarrow \infty\). Once again, we require that the signal is real, so the negative frequency coefficients are Hermitian symmetric to the positive ones: \(c_{-n} = c_n^*\). Therefore, we can rewrite the series as a combination of positive frequencies only

\[ x(t) = \Re \left(c_0 + 2\sum_{n = 1}^{n=\infty} c_n e^{ i n \omega t} \right) \]

(6.25)

where the DC constant \(c_0\) was taken out of the summation, which was multiplied by a factor of two to compensate for the energy in the negative frequencies. Now, a bandpass signal does not have a DC component, by definition, and it is in fact concentrated around the center frequency of the band \(\omega_c\). This can be expressed by rewriting the summation

\[ x(t) = \Re \left\{\left[ 2\sum_{n = 1}^{n=\infty} c_n e^{i n (\omega-\omega_c) t}\right]e^{i\omega_c t} \right\} \]

(6.26)

By comparing this expression to Eq. 6.22, we immediately see that the complex envelope is equal to the shifted Fourier series

\[ g(t) = 2\sum_{n = 1}^{n=\infty} c_n e^{ i n (\omega-\omega_c) t} \]

(6.27)

which means that its spectrum is distributed around \(\omega = 0\) and it has the bandwidth of the bandpass signal.

As was mentioned in the introduction, the complex envelope is not standard in the interpretation of the analytic signal, which is normally decomposed to a real low-frequency envelope and a fluctuating, high-frequency carrier (Dugundji, 1958). This standard definition works well only when the frequency ranges of the envelope and carrier do not breach one another (Bedrosian, 1963), although it results in some ambiguity and practical challenges notwithstanding. It appears that a formulation of the analytic signal that accepts the complex envelope may solve some of the challenges that riddle it, as is progressively being concluded in a few recent studies and will be discussed in §6.5. The complex envelope formulation, which effectively treats the carrier frequency as a constant, has been used independently of the concepts of envelope and analytic signal throughout the development of modern optics theory (e.g., Born et al., 2003; Goodman, 2017). In coherence theory, it appears to have been formally connected to the ideas of analytic signal and envelope only in hindsight (Mandel, 1967). Practically the same formulation—of a slowly varying complex amplitude—also arose in the derivation of the paraxial dispersion equation by Akhmanov et al. (1968), Akhmanov et al. (1969), which is used in the latter half of this work (§10).

The flexibility in constructing real signals by distinguishing the complex envelope and carrier domains enables us to construct high-frequency signals that carry low-frequency information using modulation⁵³. The information is assumed to vary much more slowly than the carrier and can be fully contained in a low-frequency complex envelope. The low-frequency information is then referred to as the baseband or the modulating signal, and its transformed high-frequency version is the bandpass or the modulated signal (Couch II, 2013; p. 238). It can be made to modulate either \(a(t)\)—amplitude modulation (AM) (see Figure 6.2), \(\varphi(t)\)—phase modulation, or a combination of both (AM-FM, see Figure 6.5). In this context, \(a(t)\) is called the instantaneous amplitude, and \(\varphi(t)\) is the instantaneous phase. Its derivative is the instantaneous frequency (Carson, 1922; Carson and Fry, 1937)

\[ \omega = \frac{d\varphi(t)}{dt} \]

(6.28)

which can be made to carry the information using frequency modulation (FM).

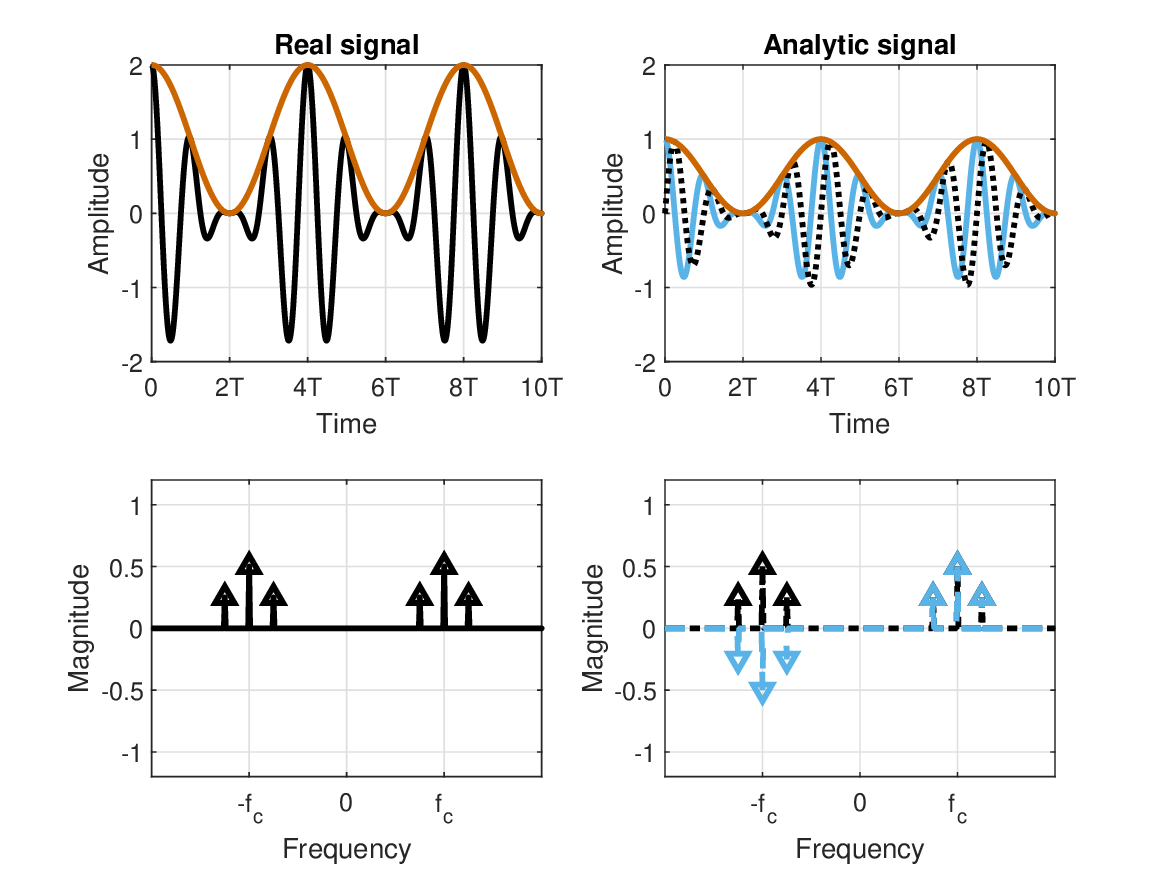
Figure 6.2: This figure is similar to Figure 6.1, only with an amplitude-modulated tone. The temporal envelopes of both real and analytic signals are plotted in red in the top plots. The spectrum contains side bands around the tone carrier. The real signal (bottom right) has the usual negative frequencies, whereas they cancel out in the analytic signal (bottom right), because of the contributions of the even (solid black) and odd spectra (dash blue).

Therefore, without loss of generality, physical communication takes place when a modulated signal of carrier frequency \(\omega_c\) and bandwidth \(\Delta \omega\) is transmitted to a receiver over a channel. The convenient properties of the bandpass system make it particularly attractive for communication, whereas wideband or even ultra-wideband may raise many technical difficulties in practice (see §5.3.1), partly because of their more ambiguous mathematical and physical nature (see §6.5).

The instantaneous quantities are readily computed from the analytic signal, as these following relations hold

\[ a(t) = \sqrt{x^2(t) + y^2(t)} = \sqrt{z(t)z^*(t)} = |z(t)| \]

(6.29)

\[ \varphi(t) = \omega_c t + \tan^{-1}\frac{y(t)}{x(t)} = \omega_c t + \tan^{-1}\left(\frac{z^*(t)-z(t)}{z^*(t)+z(t)}\right) \]

(6.30)

It will be useful to generically expand the instantaneous phase function to different terms of a power series around \(t=0\) with⁵⁴

\[ \varphi(t) = \varphi_0 + \Delta \omega t + \frac{1}{2}\Delta \dot{\omega} t^2 + \frac{1}{6}\Delta \ddot{\omega} t^3 + \cdots \]

(6.31)

We refer to the terms from left to right as phase, frequency (also, phase ramp or phase velocity), frequency velocity, frequency ramp, or phase acceleration, and the last term is frequency acceleration or phase jerk—borrowing from the naming convention in mechanics (Thompson, 2011).

6.4 Auditory envelope and phase

If the physical time signal is allowed to be completely arbitrary, then it can change equally likely in its instantaneous envelope and phase functions. Nevertheless, auditory effects of phase and envelope have been traditionally studied in isolation (e.g., measuring either AM or FM stimuli). An overarching framework for the two functions has been more prevalent over the last three decades (Rosen, 1992), although they are still largely viewed as separate entities. However, the separability of phase and envelope is not obvious if we employ the complex envelope, which requires a combination of both. In the remainder of this chapter, some of the milestones in auditory research of envelope and phase sensation are reviewed with emphasis on current trends and challenges, which will help bolster the case for using a complex envelope in hearing.

6.4.1 Auditory sensitivity to temporal envelope

The following is a brief review of a few key findings in the study of amplitude-modulated sound perception. Historical studies of envelope perception are reviewed in Kay (1982) and a modern synthesis is found in Joris et al. (2004) with emphasis on physiological findings.

While AM has been long been used as a musical effect—tremolo (tremble, in Italian)—at least since 1617 (Carter, 1991), AM as a test stimulus had been tested very sporadically until relatively recently. The first report appears to be by Alfred M. Mayer (1874), who used a perforated disc in front of a vibrating tuning fork to test at what frequency of interruptions the sound would be perceived as continuous (Figure 6.3). However, with more careful methods, it turned out that the interrupted tone never quite appears continuous, even at high modulation frequencies (Wever, 1949; pp. 408–412).

Figure 6.3: The original setup used by Mayer (1874) to test the continuity of amplitude-modulated tones that were produced by tuning forks and were interrupted by the rotating perforated disc.

Perhaps the most interesting early AM research related the significance of the speech envelope to intelligibility. AM was used in a simple apparatus for speech synthesis, the vocoder, which partially modeled the speech signal by using the level information from a bank of bandpass filters to modulate narrowband noise generators (Dudley, 1939), a principle that was simplified later and was shown to produce intelligible speech (Shannon et al., 1995). A similar principle of bandpass filter bank analysis was also used in the design of the speech spectrograph, which displayed the running level fluctuations in the speech signals in different bands (Potter, 1945; Koenig et al., 1946; Potter and Steinberg, 1950). The importance of hearing the speech envelope properly was demonstrated with the aid of the modulation transfer function (MTF). Initially introduced into acoustics as a tool to measure the interaction between the temporal envelope and the room acoustics, it showed how reverberation tends to reduce the modulation depth of received speech, which corresponds to a loss of intelligibility (Houtgast and Steeneken, 1973; Houtgast and Steeneken, 1985; see also §3.4.4). Using the analytic signal, it was later found that severe loss of intelligibility can be the result of low-pass and high-pass modulation frequency filtering of running speech signals—especially when frequencies in the range of 4–16 Hz are removed (Drullman et al., 1994b; Drullman et al., 1994a).

Modern psychoacoustic research of the perception of electronically-controlled AM may have begun with Riesz (1928). In this experiment, the audibility of beating between two sinusoidal tones was manipulated by varying the amplitudes of one of the tones, which resulted in maximum sensitivity among listeners for beating frequency of 3–4 Hz. Much of the subsequent AM research focused on the most common stimulus type, sinusoidal AM, which has been the standard throughout the literature

\[ p(t) = [1 + m\sin(\omega_m t)]\sin(\omega_c t) \]

(6.32)

The carrier frequency is set by \(\omega_c\) and the real envelope is defined by two parameters: the modulation frequency \(\omega_m\) and the modulation depth, \(0\leq m \leq1 \). It can be shown that the modulation depth can be also expressed by the minimum and maximum fluctuating intensity, \(I_{min}\) and \(I_{max}\), respectively:

\[ m = \frac{I_{max}-I_{min}}{I_{max} + I_{min}} \]

(6.33)

this expression describes the audible contrast of the modulated sound.

The perceptual sensitivity to AM was formalized with the introduction of the temporal modulation transfer function (TMTF) that directly quantifies the minimum audible modulation depth at a given modulation frequency (Viemeister, 1973; Viemeister, 1979). The sinusoidal carrier is sometimes replaced with broadband or narrowband noise, which yield different responses. The effect of the auditory filter bandwidth is clearly noticeable in sinusoidal and narrowband-noise modulation, which is not the case in broadband stimuli. The AM signal can be “resolved” to its sinusoidal components (e.g., bottom plots in Figure 6.2) when it is detected using spectral cues. It takes place when the signal is analyzed using adjacent narrow bandpass filters that are separated by less than the AM bandwidth, which results in a much improved threshold. These results will be discussed in depth in §13.4.

As may be expected from the psychoacoustic observations, envelope processing can also be traced along all the main auditory nuclei with different specificity in different cell types. Instead of varying the modulation depth as was done in the earliest studies (from Nelson et al., 1966), modern animal experiments often test the synchronization to a fully modulated (\(m=1\)) stimulus instead (beginning in Palmer, 1982), as it decreases with lower modulation depths (Joris et al., 2004). Functionally, the nonlinearity in the transduction of sound to neural discharges provides the necessary mechanism for demodulation (Khanna and Teich, 1989a; Nuttall et al., 2018).

The neurally encoded envelope is qualitatively different centrally, as a rate code—spiking patterns at the average AM frequency where instantaneous changes are no longer informative—becomes much more prevalent downstream after the inferior colliculus (IC) than the temporal code, which responds to instantaneous changes in the modulation frequency that is observable upstream(Joris et al., 2004)⁵⁵. Additionally, the maximum modulation frequency that can be gradually encoded decreases downstream from the auditory nerve, by up to an order of magnitude. It is found that some cells in the brainstem are tuned in the modulation domain and can have either a low-pass or a bandpass frequency response. While some areas are not highly specified as they synchronize to both carrier and envelope (e.g., the auditory nerve), others seem to be exceptionally geared to track the envelope information and sometimes even improve on the auditory nerve (e.g., by sharpening the response, or improving the signal-to-noise ratio).

The AM stimulus is often treated as magnitude only, without specifically considering the relative phase of the modulation. However, listeners are known to be sensitive also to modulation phase across different channels (e.g., Bregman et al., 1985; Yost and Sheft, 1989; Strickland et al., 1989; Moore et al., 1990; Lentz and Valentine, 2015), an effect that was also recorded in the auditory cortex of awake marmoset monkeys (Barbour and Wang, 2002). It appears that not all tasks are as sensitive to modulation phase changes (Lentz and Valentine, 2015), though, and not all experiments establish phase effects (Moore et al., 1991; Furukawa and Moore, 1997; Moore and Sek, 2000).

An influential theory suggests that not only is the IC organized tonotopically according to characteristic frequencies, but also according to modulation frequency, which may explain the salience of periodicity pitch (Schreiner and Langner, 1988; Langner, 1997) (see §2.4). Another influential psychoacoustic signal processing model suggests a modulation filter bank that leads to modulation channels, for which periodicity would be only a special case (Kay, 1982; Dau et al., 1997a; Jepsen et al., 2008).

6.4.2 Auditory sensitivity to phase

“Phase deafness” and its discontents

The role of phase in hearing has been much more contentious than that of the envelope. Especially, models that considered it to be immaterial for the ear seemed to have had considerable influence on the course of research and the general understanding of the ear.

In his monumental work about hearing, Helmholtz concluded the following (Helmholtz, 1948; p. 127): “...differences in musical quality of tone depend solely upon the presence and strength of partial tones, and in no respect on the differences in phase under which these partials enter into combination.” With this conclusion he had vindicated the theory of Georg Simon Ohm (1843), whose original proposal that the ear performs Fourier-series analysis on incoming complex tones was heavily criticized at the time by August Seebeck (Turner, 1977). Helmholtz spelled out Ohm's law (Helmholtz, 1948; p. 33): “Every motion of the air, then, which corresponds to a composite mass of musical tones, is, according to Ohm's law, capable of being analysed into a sum of simple pendular vibrations, and to each such single simple vibration corresponds a simple tone, sensible to the ear, and having a pitch determined by the periodic time of the corresponding motion of the air.” This is usually summarized by the idea that the ear is “phase deaf”. However, Helmholtz was almost exclusively concerned with compound “musical tones”, which lend themselves to neat interpretation as the sum of “simple tones”, limited only by the frequency resolution of the ear. All other nonperiodic and transient sounds (e.g., “jarring, scratching, soughing, whizzing, hissing”) were classified as “noise” (Helmholtz, 1948; pp. 119 and 127). Incidentally, Ohm himself never discussed the role of phase in his original paper, which makes Ohm's law a misnomer (Goldstein, 1967b; Appendix A). Helmholtz had planted the seeds of doubt notwithstanding, by carefully avoiding to make his conclusion about phase too sweeping. Referring to transient noisy sounds, he added (Helmholtz, 1948; p. 127): “we must leave it for the present doubtful whether in such dissonating tones difference of phase is an element of importance.”

Nevertheless, Helmholtz's experimental results could not be replicated and evidence for the audibility of phase had accumulated over the twentieth century (for historical reviews and results see Craig and Jeffress, 1962; Goldstein, 1967b; Plomp and Steeneken, 1969; Patterson, 1987; Moore, 2002; Laitinen et al., 2013). Typically, phase-detection experiments compared signals that have identical magnitude but different phase spectrum and documented noticeable shifts in timbre of complex tones or in masking threshold, as a consequence of their different phase spectrum. In his pulse ribbon model for phase detection, Patterson (1987) distinguished local phase effects, which stem from phase differences between adjacent unresolved frequency components that pass through the same auditory filter, from global phase effects, which correspond to timing differences across different filters (but see Laitinen et al., 2013). As all of these studies concluded, the sensitivity to local phase changes may be attributed to changes to the within-channel signal envelope rather than to the broadband spectrum associated with a pure place model. Therefore, accounting for phase effects requires temporal processing—likely based on phase locking.

Despite its incorrectness, the “phase deafness” adage has effectively transmigrated into various formulations of the power spectrum model of hearing—the necessary conclusion out of a strict place model of the cochlea, as Helmholtz theorized. In its simplest version, the power spectrum model is based on the critical-band concept discovered by Fletcher (1940), who demonstrated psychoacoustically that sound is analyzed in the ear by a bank of bandpass filters that together cover the entire audio range. Different subjective correlates have been found that correspond to the amount of energy that goes into each filter. Important applications include the pure tone audiogram (Fletcher and Wegel, 1922), the speech spectrogram (Potter, 1945; Koenig et al., 1946; Potter and Steinberg, 1950), the articulation index of speech (French and Steinberg, 1947), loudness models (Zwicker et al., 1957; Moore and Glasberg, 1987), masking models (e.g., Moore, 2013), reverberation time and other room-impulse-response indices (Kuttruff, 2017), and the modulation transfer function (Houtgast and Steeneken, 1985). Except for the speech spectrogram that is based on short-term samples, these applications rely on long-term averages of narrowband spectra of the full broadband signals, which eliminate any contribution of phase terms (see also Fant, 1970; p. 20). Perhaps it may seem surprising, then, that it is possible to reconstruct speech signals from their phase spectrum without its corresponding magnitude information, as long as some relatively general conditions hold (Oppenheim and Lim, 1981). In general, the phase spectrum contains more information than the magnitude spectrum, so that arbitrary signals suffer from smaller distortion when reconstructed from the phase spectrum alone, compared to the magnitude spectrum alone (Ni and Huo, 2007)⁵⁶.

Frequency modulation

A much more obvious type of phase change that listeners can detect is frequency modulation (FM), which entails the modulation of the phase derivative. Perhaps the most common FM stimulus in hearing research is sinusoidal modulation (sinusoidal FM) of the phase around the carrier

\[ p(t) = a \sin\left[ \omega_c t + \frac{\Delta \omega}{\omega_m} \sin(\omega_m t) \right] \]

(6.34)

where the modulation term is defined by the modulation index \(\Delta \omega / \omega_m\) and the modulation frequency \(\omega_m\). The peak frequency deviation from the carrier is \(\Delta \omega\). While periodic, this signal has a rather complicated harmonic series, whose relative amplitudes are determined by Bessel functions of the first kind, \(J_n\left( \Delta \omega/\omega_m \right)\) for harmonic \(n\) (Carson and Fry, 1937). The larger the modulation index is, the more harmonics there are with non-negligible amplitudes.

Sinusoidal FM has been used in different paradigms in hearing and only a handful are mentioned here. The musical counterpart to it is called vibrato (in analogy to tremolo for AM) and its associated perceived pitch approximately corresponds to the carrier frequency (Tiffin, 1931; Iwamiya et al., 1984). If the frequency deviation is very small, then the pitch of the carrier may sound like a pure tone, which was used to estimate the frequency discrimination associated with pure tones (Shower and Biddulph, 1931).

Different psychoacoustic results of FM recognition that depend on the modulation frequency, modulation index, duration, and occasionally on its AM envelope, suggest that different auditory signal processing may be dominant at low and high modulation frequencies. For example, some sensitivity to FM may be explainable by conversion from FM to AM, as the spiking rate in the channel that analyzes the stimulus depends on its instantaneous frequency, which corresponds to a level change that is indistinguishable from that caused by an AM signal in some conditions (Zwicker, 1952; Saberi and Haftert, 1995)⁵⁷. The span of FM signals affects several filters simultaneously, whose outputs are thought to combine to an excitation pattern that is only dependent on cochlear place—in the spirit of Helmholtz and Ohm's law (Zwicker, 1956; Moore and Sek, 1994a; Moore and Sek, 1994b). However, this view has been challenged, as the responses to some low carrier-frequency (\(<4\) kHz) and low modulation-frequency (\(<5\) Hz) stimuli appear to rely on temporal (phase) information as well (Edwards and Viemeister, 1994; Moore and Sek, 1995; Moore and Sek, 1996; Moore and Skrodzka, 2002; He et al., 2007, but see King et al., 2019). More recent modeling of AM and FM thresholds suggests that auditory processing of FM may be altogether distinct than the assumed processing for AM (Attia et al., 2021). A further possibility is that the auditory sensitivity to FM is determined centrally (perhaps cortically) by the sensitivity to the fundamental frequency (\(f_0\)) of the sound, which is primarily a function of precise place coding in the cochlea (Whiteford and Oxenham, 2023).

Physiological measurements of the auditory nerve of the cat also suggest that while the instantaneous frequency of sinusoidal FM is phase-locked to the signal, it is, in fact, converted to AM by the auditory filter (Khanna and Teich, 1989b). Different cell types of the ventral cochlear nucleus (VCN) of the guinea-pig were shown to either phase lock to the FM or to synchronize to its envelope, in a manner that depends on the characteristic frequency (CF) and the bandwidth of the cell's receptive field (Paraouty et al., 2018). In general, low-frequency VCN cells of larger bandwidth tend to phase lock to the carrier with little effect of intensity, whereas above 4 kHz, where cells also tend to be narrowband, they are synchronized primarily to the envelope. However, chopper and onset cells excel in envelope coding and do poorly in phase locking to the carrier even at low frequencies. In the different subnuclei of the cochlear nucleus of the bat, single units synchronize to maximum modulation frequency of 400–800 Hz of sinusoidal FM (Vater, 1982). In general, the degree of specialization of neurons to FM patterns increases the closer the auditory signal is to the IC (Koch and Grothe, 1998; Yue et al., 2007). Despite these findings, the low-level physiological availability of phase cues may not necessarily translate to high-level perception (Kale et al., 2014).

Linear FM is a mathematically simpler signal, but has not been studied as much as sinusoidal FM. It is defined by a single parameter—the frequency slope (or velocity) \(\Delta\dot{\omega}\)

\[ s(t) = a \sin\left( \omega_c t + \frac{\Delta \dot{\omega}}{2} t^2 \right) \]

(6.35)

where the carrier frequency \(\omega_c\) is better understood as a center frequency of a chirped pulse around \(t=0\), whose frequency slope is \(\Delta\dot{\omega} = 2\pi B /T\), where \(B\) is the bandwidth, and \(T\) is the pulse width. It can be seen that this stimulus requires band-limitation in order to contain its spectral range, which means that a specific envelope must be implemented. Thus, linear FM stimuli must involve some AM as well.

One of the most interesting features of these stimuli is that sensitivity to them is direction-dependent, as listeners exhibit lower masking thresholds to upward ramps than to downward ramps, which emphasizes the role of their phase spectrum (Nábělek, 1978; Collins and Cullen Jr, 1978). Moreover, it has been found in mammals (beginning in Whitfield, 1957 and Whitfield and Evans, 1965) that some cells in the IC and the auditory cortex are specialized in detecting particular patterns of FM (e.g., tuned to a certain bandwidth and to the direction of sweep—up or down). While these results are particularly telling about echolocating bats, they are found in different species and are thought to reflect the important role that linear FM has in vocalizations (e.g. Casseday and Covey, 1992; Klug and Grothe, 2010). Only one study appears to have tested the linear FM response at the auditory nerve level. In the auditory nerve of the cat, phase locking to the instantaneous frequency was demonstrated—both in upward and downward linear chirps (Sinex and Geisler, 1981).

Linear FM is of particular importance in this work, because of its relation to group-delay dispersion, its simplicity as a mathematical basis for arbitrary chirps, and the fact that it often leads to tractable expressions. The jargon associated with it includes many nearly-synonymous terms from different fields, which may seem obfuscating for the unacquainted reader. These terms are summarized in Table 6.1 with clarifying, informal definitions, along with near synonyms that do not necessarily imply linearity.

Term	Definition
Frequency
Linear frequency modulation (FM)	Refers to the mathematical signal or modulation technique (Eq. 6.35) that entails a linear change in the instantaneous frequency.
Glide	The term used most often in the hearing and speech/phonological literature for signals that rise or fall in frequency. It does not necessarily imply linearity, although often it is linear.
(Frequency) ramp	A linear FM signal, but with an emphasis of the upward or downward direction of the instantaneous frequency.
(Linear) sweep	Similar to a ramp, but emphasizes the coverage (either continuous or discrete) of a range of frequencies, as is often required in measurements.
(Linear) chirp	Similar to a glide, but used more often in technical literature such as signal processing and radar communication, and in the context of bat echolocation and birdsong.
Frequency velocity	The coefficient \(\Delta \dot{\omega}\) of the instantaneous frequency, or of the quadratic term of the phase (Eq. 6.31).
(Instantaneous) frequency slope	Similar to frequency velocity, but linearity is implied, at least locally.
Phase
Phase curvature	The same as frequency slope, with emphasis on the quadratic (or higher-order) term in the phase function. The term may also relate to the second-order frequency dependence of the (arbitrary) phase spectrum.
Quadratic phase	The general phase function that contains a quadratic term in frequency or time. This term is most common in Fourier optics, where the linear phase term is either omitted or treated separately.
Phase acceleration	The quadratic coefficient of the time-dependent phase function.
Group delay
Frequency-dependent group delay	The negative derivative of the phase function with respect to frequency is the group delay of the system, which is non-zero if the system is dispersive. If the second-derivative is non-zero, then the group delay is frequency dependent, which implies frequency modulation for signals that go through the system.
Group-delay dispersion (GDD)	When the group delay is frequency dependent, then it is itself dispersive. The group-delay dispersion represents this characteristic of a medium or a structure in which the wave propagates.
Group-velocity dispersion (GVD)	The group velocity and group-delay dispersions contain the same information, but GVD refers more specifically to the effect on group velocity.
Oscillators
(Long-term) frequency drift	A term that indicates a slow change in frequency that is sometimes used in oscillator modeling. A functional form is not implied, as it can be affected by random processes.
Music
Glissando	Discrete and usually rapid playing of the intermediate notes contained in the interval between two notes.
Portamento	The continuous changing (or bending) of pitch of the interval between two notes.
Vibrato	The periodic changing of the pitch around its tuning.

Table 6.1: A comprehensive list of jargon related to linear frequency-modulation used in different disciplines. Many terms do not require the FM to be strictly linear and can be synonymous in some contexts. The phase- and group-delay terms imply (linear) FM indirectly. Most terms do not have a closed definition, so their definitions here are provided according to the best understanding of the author.

6.4.3 The envelope and the temporal fine structure

Despite the evident link between the temporal envelope and the phase spectrum, until recently they have been framed in research largely as separate entities. Using the unified framework of the analytic signal, a more recent trend in research has started juxtaposing the slow-varying envelope and the rapid phase changes—the temporal fine structure (TFS). Rosen (1992) defined the TFS as “...variations of wave shape within single periods of periodic sounds, or over short time intervals of aperiodic ones as fine-structure information.” The envelope was defined there as: “fluctuations in overall amplitude at rates between about 2 and 50 Hz as envelope information”⁵⁸. This approach is consistent with hearing research that has not adopted the idea of complex envelope, but instead has applied the standard analytic-function real envelope with positive frequencies⁵⁹.

The analytic signal hypothetically enables the separation of the envelope and the TFS from an arbitrary signal. This idea has been applied several times to illustrate how different aspects of the auditory signal processing may be dominated by one or the other. For example, speech intelligibility appears to be dominated by the temporal envelope (Drullman et al., 1994a; Drullman et al., 1994b), even when the TFS is removed (Shannon et al., 1995; Smith et al., 2002; Zeng et al., 2005). In contrast, the TFS appears to be important in sound localization and pitch (melody and tonal vowels) perception (Smith et al., 2002; Xu and Pfingst, 2003), voice identification and intelligibility with competing speech (Zeng et al., 2005), and listening in the dips (Lorenzi et al., 2006). However, the underlying methods have been challenged for being mathematically unsound (see §6.5), as the information in the discarded part (the envelope or the TFS) is in fact preserved in the remaining part. Indeed, speech intelligibility in quiet is also rich with TFS-only cues (Lorenzi et al., 2006).

6.4.4 A final remark

The partial reviews above reveal a complex interplay between the envelope and phase functions with respect to the auditory perceptual roles they realize. However, it is not intuitively obvious why some situations and stimuli can be processed, ostensibly, with no phase information, whereas in other cases the phase either contains either an equal amount or most of the information. In order to be able to answer this question, a coherence theory is required that is suitable for auditory processing, which makes a distinction between coherent, partially coherent, and incoherent signals. This distinction delineates the signals for which processing the phase matters and those that do not. Essentially, these provide the basic conditions for phase locking (processing of TFS) to be altogether possible and, beyond that, useful. The foundations of such a theory are presented in §7, §8, and §9.

6.5 Challenges to the analytic signal formulation

Even though the analytic signal decomposition is unique, applying it universally to arbitrary signals is not without complications. This section reviews some of these challenges from different interrelated perspectives: mathematical, auditory, and conceptual. While the importance of the challenges to the interpretation of various results is yet unclear, they reflect a real engineering problem that the hearing system has to routinely solve: to construct unambiguous perceptual representations of broadband signals that are not mathematically unique.

6.5.1 Auditory challenges

Empirical methods

As was noted in §6.4.3, the standard analytic signal is often employed to obtain an estimate of the real envelope and TFS. So, for example, one common method has been to resynthesize signals using decompositions to envelope and TFS, which can be manipulated independently (e.g., Drullman et al., 1994b; Drullman et al., 1994a; Smith et al., 2002; Zeng et al., 2005; Lorenzi et al., 2006). However, this procedure has been criticized on several grounds. Ghitza (2001) demonstrated how the envelope information is regenerated from a Hilbert-transformed signal, which was supposed to retain only TFS information. These results were confirmed physiologically from auditory nerve measurements in the chinchilla (Heinz and Swaminathan, 2009). Schimmel and Atlas (2005) showed how the sub-band (i.e., narrowband filter bank) decomposition of arbitrary signals to a carrier and a real envelope is both contrived and incomplete, as it requires the modulated signals to be symmetrical around the filter center frequency—an unrealistic assumption⁶⁰. Instead, they suggested a two-dimensional bi-frequency decomposition (carrier and modulation frequencies) which includes complex envelope modulation (see also Atlas and Shamma, 2003 for a discussion about the bi-frequency decomposition relevant to audio signals). Apoux et al. (2011) built on these findings and emphasized how envelope and TFS manipulation that is suitable for synthetically produced analytic signals cannot be generalized to arbitrary signals, such as natural speech. The authors demonstrated how when the assumption of real non-negative envelope is used to decompose signals with a negative envelope, wideband TFS-only signals that span several critical bands become contaminated with envelope information in multiple sub-bands. Importantly, these findings were not specific for Hilbert decomposition and were shown for another envelope extraction technique (squared, low-pass filtered, half-wave rectification)⁶¹.

According to the definition of the analytic signal, the low-frequency amplitude and phase—the components of the complex envelope—are not meant to be independent. Rather, it is the real and imaginary parts of the signal that are separable and even they constrain one another (at least long term). The polar representation of complex functions is neither unique nor separable and both amplitude and phase are dependent on the real and imaginary values of the function, as is seen from Eqs. 6.29 and 6.30 (see also Boashash, 1992 and Picinbono, 1997). While it casts a doubt on some past claims in studies that found high speech intelligibility after removing the envelope or TFS information (e.g., Smith et al., 2002; Lorenzi et al., 2006), it is noteworthy that they produced meaningful results that appear to be relatively robust to variations and consistent with research based on other methods (Gilbert and Lorenzi, 2006; Sheft et al., 2008; Moore, 2008; Moore, 2019).

Bandwidth

As was emphasized throughout this chapter, the analytic signal relies on the narrowband approximation, as are the majority of communication systems. But, while individual auditory channels are narrowband, the overall audio bandwidth is ultra-wideband (see §6.6 below). Additionally, due to the low frequencies involved, there is a large overlap between the overall low-frequency audio and modulation spectra (see Table §1.2 and Figure 2 in Joris et al., 2004)⁶². When signals are modulated within individual filters, the two spectra are independent and they are perceived in qualitatively different manner, so they are unambiguous. However, if the modulation frequency (in AM) or maximum frequency deviation (in sinusoidal FM) are large enough to be resolved by adjacent filters, then the modulation components disappear from the perceived modulation spectrum and appear in the audio spectrum. Conversely, when spectral components are too close to be resolved, they may beat—appear as modulation instead of two individual pitches. Therefore, this interdependence between the two domains is dictated by the auditory filter bandwidths throughout the spectrum. It means that the physical information that produces the acoustic vibrations is conserved either in the audio or in the modulation domain, but may not necessarily correspond to the physical mechanism that produced it, which may be either a mode of vibration or modulation, but not both (see §3). It also means that if signals are dramatically scaled either spectrally or temporally, they may undergo qualitative perceptual changes that render the message they carry less recognizable, as different components move between the two spectra.

This challenge is not unique to the analytic signal framework, but it is made especially pertinent because of its predication on narrowband signals.

6.5.2 Mathematical challenges

As was noted earlier, the analytic signal prescribes a unique combination of real and imaginary signals, which do not necessarily translate to unique amplitude and phase, once converted to polar representation. As the amplitude function determines the degree of AM and the phase function determines the FM, complex AM-FM signals may not be uniquely decomposable, which makes their decomposition an ill-posed problem. Loughlin and Tacer (1996) suggested a method to uniquely determine the AM-FM while satisfying these four conditions (cf. Vakman, 1996): signal level boundedness must stem from the AM part, bandwidth limitation must apply to the FM, pure tones entail constant AM and FM, and level scaling applies to AM but not to FM. These conditions are very reasonable, as long as the system is linear. The solution Loughlin and Tacer proposed is based on the complex envelope, effectively (see also Atlas et al., 2004). The carrier is obtained from the time-frequency distribution, which can be used to coherently demodulate the signal (e.g., by subtracting its carrier; see §5.3.1). Cohen et al. (1999) further explored the problem and proposed that it may be resolved either with a non-negative amplitude and occasionally a discontinuous phase, or by forcing continuous phase and accepting the existence of negative amplitudes. The latter solution can be made to work as a complex envelope. However, the conclusion that the analytic signal produced ambiguous instantaneous quantities was criticized by Hahn (2003), who showed that by using complex phase and frequency functions the ambiguity disappears. While mathematically correct, it requires us to embrace these complex functions that are not particularly intuitive. Additionally, it does not solve the auditory challenges (§6.5.1) that were observed after the analytic signal was applied to separate the TFS and envelope.

Broadband signals pose an even more challenging problem than narrowband signals, as they do not have a unique representation that is based on specific decomposition (e.g., Boashash, 1992). The perceived signal must be the end-result of a combination of outputs from all the active auditory filters, which gives rise to the auditory experience. This has led to the development of different time-frequency analysis methods that are capable of extracting the narrowband frequencies from broadband signals—often still resorting to the analytic signal along the process (Huang et al., 2009).

An additional challenge for analytic signals has to do with nonstationarity and is briefly mentioned in §8.2.9.

6.5.3 Frequency and instantaneous frequency

The concept of instantaneous frequency was presented earlier, in passing, where it was defined as the derivative of the phase with respect to time. For a pure tone that has a linear phase function, the frequency is a constant and is exactly equal to the instantaneous frequency. However, standard frequency, as is obtained from Fourier analysis of time signals, measures repeating patterns over the entire duration of the signal from minus to plus infinity, but is not time dependent in itself. For example, an arbitrary FM signal can be expressed in the form

\[ x(t) = a \exp \left[ i\left(\omega_c t + \gamma \int_{-\infty}^t m(\tau) d\tau \right)\right] \]

(6.36)

the instantaneous frequency being \(\omega_c + \gamma m(t)\), which describes the frequency deviation from the fixed carrier frequency. For any \(m(t)\) that is non-constant, \(x(t)\) is probably not going to be periodic.

How is one to understand the meaning of an instantaneous frequency function that describes a fluctuation that need not be periodic? The conceptual discrepancy between the two frequency definitions was noted already by Carson (1922) in his early work on FM and has been debated ever since (Boashash, 1992; Cohen, 1995; pp. 39–41). Gabor (1946) echoed this question when he introduced the analytic signal and noted that our auditory perceptual intuition does not necessarily coincide with the traditional Fourier view of frequency, which is much more rigid than the common perceptual experience of time-varying frequencies. Rather, he noted, our hearing experience lies somewhere in between the steady-state Fourier frequency and the instantaneous one. An ad-hoc solution in numerous auditory models and other acoustic applications has been to use some variation of the short-time Fourier transform, which is integrated over short (overlapping) time windows. This retains short periods of constant spectrum, which can be merged together into a continuous signal, when the time windows are partially overlapping.

As long as the narrowband approximation is carefully maintained, the instantaneous frequency appears to have a plausible physical meaning as the deviation from the carrier (plus the carrier) (Boashash, 1992). Other useful definitions exist, then, which may provide further intuition. For example, the instantaneous frequency is the first frequency moment of the time-frequency distribution of the signal, such as the Wigner-Ville distribution. Or, for a monotonic instantaneous frequency and large time-bandwidth product, it also determines the group delay of the signal as a function of frequency (also defined locally for a narrowband signal; see §3.2).

Importantly, the instantaneous frequency loses any coherent meaning for broadband and multicomponent signals. This situation is particularly delicate, because multicomponent signals do not have a unique representation in terms of variable components, if they intersect on the time-frequency plane. This is the reason why, in general, broadband signals do not have a unique representation. An example from Boashash (1992) that illustrates this situation for two components is reproduced in Figure 6.4. Nevertheless, long and broad sweeps, for example, do not sound ambiguous, so the instantaneous frequency has a role there that extends beyond a single narrowband filter. The instantaneous frequency is also indispensable in nonlinear and nonstationary systems, where the Fourier transform is generally invalid (Huang et al., 1998; Huang et al., 2009; see also §3.2).

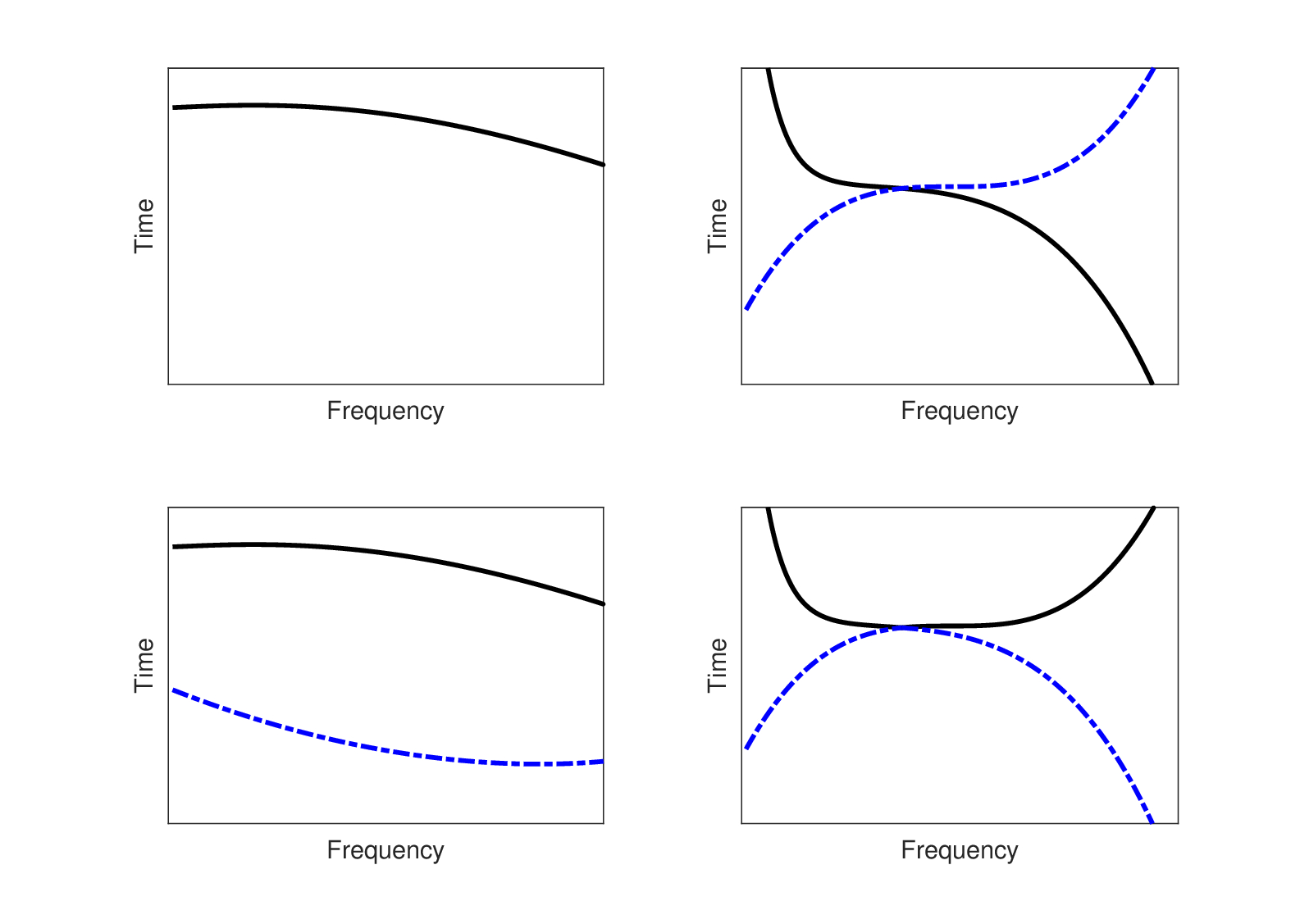
Figure 6.4: Different types of signals qualitatively plotted on the time-frequency phase plane. Top left: A monochromatic signal can be unambiguously described in terms of its time-frequency distribution, although it has to be narrowband in order for the instantaneous frequency to be meaningful. Bottom left: A multicomponent signal with two components that can be described unambiguously, since their trajectories do not intersect. Top and bottom right: A multicomponent signal with two components, whose trajectories intersect, is ambiguous in terms of which trajectory belongs to which component. This figure is based on Figures 3 and 13 from Boashash (1992).

6.6 Hearing, modulation, and demodulation

6.6.1 Real and complex envelopes

The difference between real (standard auditory interpretation) and complex (nonstandard) envelopes is in the phase term. The complex envelope includes the frequency deviation around the carrier, which is treated as a constant that is subtracted from the total frequency. Thus, the spectrum of the complex envelope is double-sided and generally includes negative frequencies. A real envelope function is obtained only when the spectrum is Hermitian-symmetrical, which requires precise subtraction of the carrier. So, when the real envelope representation is employed, the carrier is taken to be part of the TFS, which leaves the phase modulation in the bandpass domain. Mathematically, this difference can be thought of as two different ways to associate the signal components. Using the complex envelope, the signal is \(\Re\left\{[a(t)e^{i\varphi(t)}] \cdot [e^{-i\omega_c t}]\right\}\), whereas the real-envelope signal is \(\Re\left\{|a(t)| \cdot [e^{-i\omega_c t+i\varphi(t)}]\right\}\) (see Figure 6.5 for an illustration) (cf., Shekel, 1953). In other words, according to this standard view of hearing science, the auditory system does not necessarily demodulate the incoming signal phase. To the extent that any demodulation takes place, it occurs only in amplitude, which can theoretically happen noncoherently (without the phase information, or precise knowledge of the carrier; see §5.3.1).

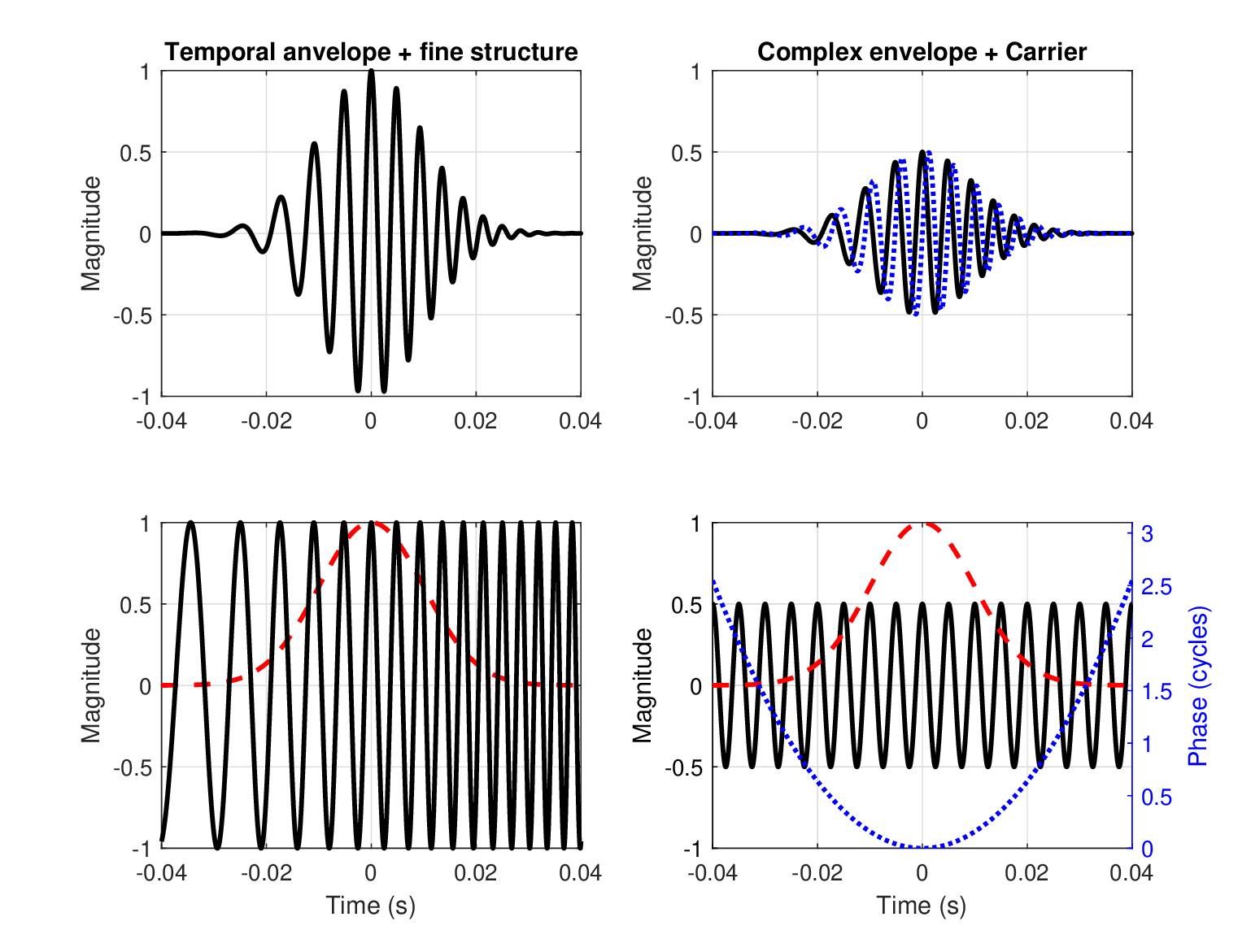
Figure 6.5: The real time-signal of a linear chirp (top left) and its analytic signal representation—real and imaginary parts (top right). In the bottom figures, two decompositions of the signals are displayed. Bottom left: The standard auditory decomposition to a real envelope and temporal fine structure. Bottom right: The complex envelope and carrier of the analytic signal. The complex envelope is displayed as magnitude (dash red) and unwrapped phase in cycles (dotted black). The constant carrier is in solid black.

There is another important difference that the complex envelope and the demodulation process emphasize, which the real envelope approach tends to overlook. Modulation is about changes from the mean—the mean being the static carrier amplitude and frequency. Thus, expressing the changes from the mean is much more efficiently done with low modulation frequencies rather than high frequencies, as it requires a smaller amount of information to be communicated between the transmitter and the receiver. The low-frequency deviation of FM, which the complex envelope isolates from the carrier along with AM frequencies, may be sampled at a low rate, effectively achieving lossless compression. It is impossible to take advantage of this economy when the fast high-frequency changes in the TFS are those that are being communicated.

Whether the TFS is demodulated or not, a complex envelope representation is more general, as it retains the option for noncoherent detection. Indeed, some hearing research trends suggest that a conceptual transition from real to complex envelope may be timely. The significance of the TFS information (as currently defined) in normal hearing is gradually understood to be critical to many of its functions (Moore, 2008; Moore, 2014; Moore, 2019). At the same time, there may be a warming up to the idea of auditory demodulation, especially when the baseband components can be directly identified in the system (e.g., Khanna and Teich, 1989a; Khanna and Teich, 1989b; Teager and Teager, 1990; Feth, 1992; Khanna and Hao, 2001; Khanna, 2002; Cooper, 2006; Nuttall et al., 2018). The hypothesis that AM and FM may be centrally coded in the same channel, which depends only on the modulation frequency of either AM or in FM, is also notionally closer to the demodulation idea (Moore et al., 1991). In animals such as bats, whose audible bandwidth can reach up to 100 kHz, modulation of very high-frequency carriers is standard so that synchronization can only happen in baseband—effectively after the signal has been noncoherently demodulated (e.g., Vater, 1982; Bodenhamer and Pollak, 1983). As was implied in §6.5, the analysis of these cases may benefit from the intuitive appeal of the complex envelope, which appears to have the potential to solve at least some of the mathematical difficulties associated with real envelopes. A complex envelope (even when this term is not used explicitly) seems to better represent practical problems in hearing, such as estimating the fundamental frequency of speech through frequency-following response (FFR; Aiken and Picton, 2006), or accounting for the effects on speech intelligibility of differential envelope delay or time reversal, which are applied to different bands of the broadband speech spectrum (Greenberg et al., 1998; Greenberg and Arai, 2001). Importantly, the complex envelope as a mathematical tool also coincides with the common complex amplitude or phasor formalism that is used throughout wave physics, including most of those that are used later in this work. This may enable a more intuitive interpretation of some solutions, which are readily understood to be separable to carrier and modulation domain information⁶³.

It must be remembered that this discussion merely relates to different ways to represent signals mathematically, which ultimately all map the very same real physical signal. However, different representations may better correspond to different perceptual counterparts produced by the hearing system.

6.6.2 Two spectra

Aside from phase deafness, Helmholtz's legacy reflects an additional important cause that may be implicated in the predominance of a real envelope interpretation that is divorced from true demodulation—as is the norm in hearing science. Ever since ancient Greece, knowledge in acoustics was intertwined with musical understanding—of intervals, tuning, instruments, consonance, dissonance, etc. (Hunt, 1992). The scientific and mathematical advents of the 19th century—mainly Fourier's theory—provided appealing solutions to simple vibrating systems and, as Ohm proposed, had a high explanatory power for a more general range of problems. However, without fail, the emphasis throughout has been tones, both simple and complex—how they interact, or how musical they sound. Pitch, according to this view, is the ultimate acoustical percept. Because pure-tone pitch (rather than periodicity, residue, or binaural pitches) is determined primarily by frequency, it is perhaps reasonable that precise spectrum analysis, as implied by the pure place model, is the most important aspect of hearing. It is natural then that frequency resolution becomes key to understand auditory perception and design. For example, Zweig et al. (1976) discussed the “cochlear compromise” of the cochlear mechanical design, which entails a trade-off between minimal reflection of sound and maximal spectral resolution. Extrapolating from this perspective, envelope detection becomes a secondary feature of the system, which can use it to extract additional information from the signal that relates the varying level of specific spectral components. Furthermore, if the signal information is mainly in its magnitude spectrum, then modulating it is an extra layer of information that is optional. This logic entails that the signal does not have to be demodulated, because there may be no underlying message to be received, aside from the spectrum itself. However, if the modulation spectrum is equally important as the audio spectrum, then it is not at all obvious that a very sharp frequency resolution is the correct design goal for the system.

Let us compare the auditory filter design problem with that of generic communication and optical imaging systems. In standard communication (of a single carrier), it is the low-frequency information that is of the ultimate importance (e.g., the message). It modulates a somewhat arbitrary carrier, which is selected according to its physical properties and can address different requirements of information transmission: What is the required channel bandwidth? How much energy is required to generate the carrier? How far can it travel? How noisy does it become? How much interference is it subjected to by competing transmissions? How much error does it typically accumulate? How complicated is it to modulate and demodulate these frequencies? And so forth. However, once the carrier is received and demodulated, its role is over and it does not hold any additional information but its very own channel identity⁶⁴.

In optical imaging, as in the eye, the image is the modulation pattern—the complex envelope that is manifest in colors, which are analogous to pitch. Light energy is carried at frequencies that cannot be biologically tracked and are immediately demodulated in the retina. The color—really, the visual channel—obviously carries some information (similar to cochlear place information). But a colorless (black and white) image still contains much of the optical information. Either way, just as in other communication systems, the message is contained in the (complex) envelope patterns, which modulate the light. Therefore, visual imaging can be understood as a form of communication, as was argued in §5.4.

Given the finite bandwidth of the auditory system—its very low (\(f_L = 20\) Hz) and not very high (\(f_H = 20\) kHz) cutoff frequencies—its inputs and outputs are often treated as baseband signals that can be directly sampled without demodulation, e.g., at a sampling rate of 44.1 kHz, which samples all frequencies from 0 Hz. For example, Fastl and Zwicker (2007, p. 158) conveniently assume that the lowest critical band runs from 0 Hz, or Oppenheim and Lim (1981) directly compares processing the speech audio phase spectrum to a visual image modulation phase spectrum. This switch from bandpass to baseband signaling can only be done because of the relatively low frequencies involved in hearing, but it would be out of the question if they were much higher. Informationally speaking, however, it is wrong, since hearing is a true bandpass system.

One may ask, then, why hearing is any different from standard communication systems? After all, it is certainly used for communication, so is there any particular reason why it should not be configured as a communication system? One answer may have to do with the fact that the ear contains many more channels than the eye, or most typical radio receivers. It allows for very rich spectral coding, for which the modulation information is relatively secondary. However, even as a classical spectrum analyzer or pitch interpreter, it still has to acquire the onsets and offsets of the different tones, as well as their varying levels. These can all be thought of as AM envelope functions, without any loss of generality (e.g., Kay, 1982).

A related argument for why hearing is different from other communication systems is that it clearly violates the narrowband approximation, if all the channels are considered en masse rather than individually. Thus, the human ear may be more usefully classified as an ultra-wideband (UWB) system, which can be defined somewhat differently according to the application. In radar systems, for example, an UBW system is said to have a relative bandwidth that satisfies \((f_H-f_L)/(f_H+f_L) \geq 0.25\) (Taylor, 1995; p. 2), which for human hearing is close to unity(!). In communication systems, UBW systems are defined by having bandwidth larger than 20% of the center frequency (Arslan et al., 2006; p. 11)—a limit that is breached in hearing no matter how the center frequency is defined. Similarly engineered systems to hearing may exist in impulse radio or multiband UBW communication systems—two UBW techniques which distribute the large bandwidth in pulse trains, or divide the signal into several carriers, respectively (Arslan et al., 2006; pp. 11-12). The same bandwidth criteria for UWB systems are also applied in optical communication (Yao et al., 2007). Thus, as a communication system, hearing appears to have a peculiar design that may well qualify as UBW.

Because the carrier-centered and envelope-centered perspectives on hearing are complementary points of view, deciding which one is more faithful to the system's internal logic may seem like a moot exercise. Nevertheless, the envelope-centered perspective—that of true modulation—would imply that the specific identity of the carrier—the exact pitch—is of secondary importance. If the same message can modulate different carrier(s) and it can be decoded equally well, then it would strongly support an envelope-centered perspective. This “spectrum-invariance” is indeed the case often—within some constraints—as a verbal message can be equally well received if spoken by two different voices of different fundamental and formant frequencies, or a musical piece can be similarly well-received if it is played for different arrangements and in different keys. This does not diminish from the importance of spectral range and across-channel periodicity effects that are uniquely auditory. And indeed, music and speech can be equally well perceived also at different tempi, which entails scaling of the low-frequency envelope, but not of the carrier spectrum. Therefore, there is a broad category of messages that appears to be relatively invariant to both spectral and temporal changes, which suggests that the auditory system simultaneously extracts information from at least two dimensions. It also suggests that the system may not be constrained to the spectrum nor to the complex envelope, as long as the acoustic information can be extracted from one of them, or from the combination of both.

Footnotes

50. The term “analytic signal” was coined by Jean Ville (1948).

51. See Nussenzveig (1972, pp. 389–390) for a rigorous derivation of this expression.

52. Another definition was proposed in §3.2.2 based on dispersion, which may be more intuitive when frequency-dependent group delay is taken into consideration: A narrowband range of frequencies is taken such that the group delay changes only a little from its mean value at the center frequency of the band (the carrier).

53. Of course, modulated signals can be formed by real envelopes and fluctuating carriers, as there is ambiguity in the definition. But we shall usually refer to the complex envelope formulations.

54. This useful nomenclature was presented by Mark Wickert in http://ece.uccs.edu/~mwickert/ece5675/ without reference, but these terms occasionally appear in literature.

55. The distinction between temporal and rate encoding is discussed in Theunissen and Miller (1995). Note that even if rate coding is more prevalent downstream, variations of spiking patterns around the mean can still carry information (Qasim et al., 2021).

56. It is worth noting that there are serious practical difficulties in obtaining the phase spectrum of arbitrary signals using standard methods for acoustic signal processing (e.g., using the phase obtained by short-time Fourier transforms), primarily due to phase wrapping and truncation effects of signal windowing. Modern techniques for overcoming these challenges have been an active field of research in the signal processing of speech (Mowlaee et al., 2016).

57. The opposite conversion—between AM and PM—has been recently demonstrated in humans, where the level-dependent phase response of amplitude-modulated otoacoustic emissions was shown to correlate with the sensitivity to AM, at frequencies where phase locking was available (Otsuka and Furukawa, 2021).

58. In a footnote (p. 74), Rosen noted that this definition is not the same as the envelope of the analytic signal, although the two are related. This assertion is attributed to findings by Seggie (1986), but it is not clear why this is the case. At present, the community appears to treat the envelope as in the analytic signal (e.g. Moore, 2008).

59. It is curious to note that the conceptual origins of the analytic signal and the temporal fine structure are both rooted in quantum mechanics. The analytic signal was introduced by Gabor (1946), who used the complex quantum wave function formalism to try and establish the uncertainty relations in hearing, similarly to the ones from quantum mechanics (Heisenberg, 1927). The “fine-structure constant” was introduced in quantum mechanics by Arnold Sommerfeld in 1915–1916, who used it to account for the spectral line splitting of the hydrogen atom, due to relativistic and spin effects (Kragh, 2003). It was probably imported to hearing science by Licklider (1952), who was also trained as a physicist. Many of the famous results in quantum mechanics are based on stationary wavefunctions that are time-independent, as harmonic solutions to Schrödinger's equation are assumed. In these cases, the power spectrum is the only measurable property, and the phase cancels out. Gabor too suggested (in a footnote) that Ohm's law for hearing holds, yet his analytic signal accounted for the phase notwithstanding and therefore became a much more general tool than what it was originally developed for.

60. Another way to frame it is to say that the carrier frequency must be precisely estimated at all times. This requires some kind of phase locking mechanism (Clark, 2012).

61. It is interesting to note that a similar discussion is ongoing in neuroscience, where cortical synchrony may be quantified purely temporally (by measuring phase locking), or both temporally and amplitudinally (using coherence) (Lachaux et al., 1999). However, in order for this separation to be meaningful, the frequency range has to be narrowband and even then it is not obvious that the two measures are truly independent (Srinath and Ray, 2014; Lepage and Vijayan, 2017). These concepts will be discussed with relation to hearing in §7, §8, and §9.

62. Depending on the spectral resolution, noise, and complexity of the signals and detector involved, the modulation can appear as sidebands in the spectrum around the main lobe, or broaden the spectral bandwidth of the center frequency. Modulation frequencies, though, constitute an additional dimension to the signal and are sometimes thought of as hidden, as they cannot be straightforwardly detected using normal spectral analysis. Instead, detecting them requires so-called cyclostationary techniques, such as autocorrelation (Gardner, 1988; Gardner, 1991; Antoni, 2009). Demodulation can be seen as a rather specific cyclostationary application that targets a specific channel and does not necessarily aims to measure the specific spectral modulation content at its output.

63. While approached from a numerical perspective without reference to the mathematically complexity of the envelope, a recent computational model of cochlear processing using the envelope as its primary object has shown an impressive predictive power for several key auditory phenomena, including an effective extraction of the auditory filter responses (Thoret et al., 2023). It relies on a variation of the empirical mode decomposition algorithm (limited to a single iteration), which separates the upper and lower envelopes and inherits the periodicity contained in both (Huang et al., 1998). While not referred to as complex envelope, this method retains all the information in the signal—notably any asymmetry that is contained in its envelope—which is equivalent to using the complex envelope of the signal minus the static carrier signal. This procedure is indeed expected to be most suitable for dealing with nonstationary “improper” real-world signals (§8.2.9).

64. Incidentally, a general and modality-independent neural model suggested that communication between neurons in the thalamus and cortex does exactly what we would expect it to do according to the communication theory: it rate-codes only the channel identity, while it temporally-codes the actual message (Hoppensteadt and Izhikevich, 1998).

References

Aiken, Steven J and Picton, Terence W. Envelope following responses to natural vowels. Audiology and Neurotology, 11 (4): 213–232, 2006.

Akhmanov, SA, Chirkin, AS, Drabovich, KN, Kovrigin, AI, Khokhlov, RV, and Sukhorukov, AP. Nonstationary nonlinear optical effects and ultrashort light pulse formation. IEEE Journal of Quantum Electronics, QE-4 (10): 598–605, 1968.

Akhmanov, SA, Sukhorukov, AP, and Chirkin, AS. Nonstationary phenomena and space-time analogy in nonlinear physics. Soviet Physics JETP, 28 (4): 748–757, 1969.

Antoni, Jérôme. Cyclostationarity by examples. Mechanical Systems and Signal Processing, 23 (4): 987–1036, 2009.

Apoux, Frédéric, Millman, Rebecca E, Viemeister, Neal F, Brown, Christopher A, and Bacon, Sid P. On the mechanisms involved in the recovery of envelope information from temporal fine structure. The Journal of the Acoustical Society of America, 130 (1): 273–282, 2011.

Arslan, Hüseyin, Chen, Zhi Ning, and Di Benedetto, Maria-Gabriella. Ultra Wideband Wireless Communication. John Wiley & Sons, Inc., Hoboken, NJ, 2006.

Atlas, Les and Shamma, Shihab A. Joint acoustic and modulation frequency. EURASIP Journal on Applied Signal Processing, 2003: 668–675, 2003.

Atlas, Les, Li, Qin, and Thompson, Jeffrey. Homomorphic modulation spectra. In IEEE International Conference on Acoustics, Speech, and Signal Processing, volume 2, pages II–761–II–764. IEEE, 2004.

Attia, Sarah, King, Andrew, Varnet, Léo, Ponsot, Emmanuel, and Lorenzi, Christian. Double-pass consistency for amplitude-and frequency-modulation detection in normal-hearing listeners. The Journal of the Acoustical Society of America, 150 (5): 3631–3647, 2021.

Barbour, Dennis L and Wang, Xiaoqin. Temporal coherence sensitivity in auditory cortex. Journal of Neurophysiology, 88 (5): 2684–2699, 2002.

Bedrosian, Edward. A product theorem for Hilbert transforms. Proceedings of the IEEE, 51 (5): 868–869, 1963.

Békésy, Georg von. Some biophysical experiments from fifty years ago. Annual Review of Physiology, 36 (1): 1–18, 1974.

Boashash, Boualem. Estimating and interpreting the instantaneous frequency of a signal. I. Fundamentals. Proceedings of the IEEE, 80 (4): 520–538, 1992.

Bodenhamer, Robert D and Pollak, George D. Response characteristics of single units in the inferior colliculus of mustache bats to sinusoidally frequency modulated signals. Journal of comparative physiology, 153 (1): 67–79, 1983.

Born, Max, Wolf, Emil, Bhatia, A. B., Clemmow, P. C., Gabor, D., Stokes, A. R., Taylor, A. M., Wayman, P. A., and Wilcock, W. L. Principles of Optics. Cambridge University Press, 7th (expanded) edition, 2003.

Bregman, Albert S, Abramson, Jack, Doehring, Peter, and Darwin, Christopher J. Spectral integration based on common amplitude modulation. Perception & Psychophysics, 37 (5): 483–493, 1985.

Carson, John R. Notes on the theory of modulation. Proceedings of the Institute of Radio Engineers, 10 (1): 57–64, 1922.

Carson, John R and Fry, Thornton C. Variable frequency electric circuit theory with application to the theory of frequency-modulation. Bell System Technical Journal, 16 (4): 513–540, 1937.

Carter, Stewart. The string tremolo in the 17th century. Early Music, 19 (1): 43–60, 1991.

Casseday, JH and Covey, Ellen. Frequency tuning properties of neurons in the inferior colliculus of an fm bat. Journal of Comparative Neurology, 319 (1): 34–50, 1992.

Clark, Charles Pascal. Coherent demodulation of nonstationary random processes. PhD thesis, University of Washington, 2012.

Cohen, Leon. Time-Frequency Analysis. Prentice Hall PTR, Upper Saddle River, NJ, 1995.

Cohen, Leon, Loughlin, Patrick, and Vakman, David. On an ambiguity in the definition of the amplitude and phase of a signal. Signal Processing, 79 (3): 301–307, 1999.

Collins, M Jane and Cullen Jr, John K. Temporal integration of tone glides. The Journal of the Acoustical Society of America, 63 (2): 469–473, 1978.

Cooper, Nigel P. Mechanical preprocessing of amplitude-modulated sounds in the apex of the cochlea. ORL, 68 (6): 353–358, 2006.

Couch II, Leon W. Digital and Analog Communication Systems. Pearson Education Inc., Upper Saddle River, NJ, 8th edition, 2013.

Craig, James H and Jeffress, Lloyd A. Effect of phase on the quality of a two-component tone. The Journal of the Acoustical Society of America, 34 (11): 1752–1760, 1962.

Dau, Torsten, Kollmeier, Birger, and Kohlrausch, Armin. Modeling auditory processing of amplitude modulation. I. Detection and masking with narrow-band carriers. The Journal of the Acoustical Society of America, 102 (5): 2892–2905, 1997a.

Drullman, Rob, Festen, Joost M, and Plomp, Reinier. Effect of temporal envelope smearing on speech reception. The Journal of the Acoustical Society of America, 95 (2): 1053–1064, 1994a.

Drullman, Rob, Festen, Joost M, and Plomp, Reinier. Effect of reducing slow temporal modulations on speech reception. The Journal of the Acoustical Society of America, 95 (5): 2670–2680, 1994b.

Dudley, Homer. Remaking speech. The Journal of the Acoustical Society of America, 11 (2): 169–177, 1939.

Dugundji, J. Envelopes and pre-envelopes of real waveforms. IRE Transactions on Information Theory, 4 (1): 53–57, 1958.

Edwards, Brent W and Viemeister, Neal F. Frequency modulation versus amplitude modulation discrimination: Evidence for a second frequency modulation encoding mechanism. The Journal of the Acoustical Society of America, 96 (2): 733–740, 1994.

Fant, Gunnar. Acoustic Theory of Speech Production. Mouton, The Hague, Netherlands, 1970. First printing in 1960.

Fastl, Hugo and Zwicker, Eberhard. Psychoacoustics: Facts and Models. Springer Science & Business Media, 3rd edition, 2007.

Feth, Lawrence L. Demodulation processes in auditory perception. Technical Report Final Report, 1 Dec. 1988-31 May 1992, Ohio State University, Division of Speech and Hearing Science; Air Force Office of Scientific Research, 1992.

Fletcher, Harvey and Wegel, Robert L. The frequency-sensitivity of normal ears. Physical Review, 19 (6): 553, 1922.

Fletcher, Harvey. Auditory patterns. Reviews of Modern Physics, 12 (1): 47–65, 1940.

French, Norman R and Steinberg, John C. Factors governing the intelligibility of speech sounds. The Journal of the Acoustical Society of America, 19 (1): 90–119, 1947.

Furukawa, Shigeto and Moore, Brian CJ. Effect of the relative phase of amplitude modulation on the detection of modulation on two carriers. The Journal of the Acoustical Society of America, 102 (6): 3657–3664, 1997.

Gabor, Dennis. Theory of communication. Part 1: The analysis of information. Journal of the Institution of Electrical Engineers-Part III: Radio and Communication Engineering, 93 (26): 429–457, 1946.

Gardner, William A. Statistical Spectral Analysis: A Nonprobabilistic Theory. Prentice Hall, Inc., Englewood Cliffs, NJ, 1988.

Gardner, William A. Exploitation of spectral redundancy in cyclostationary signals. IEEE Signal Processing Magazine, 8 (2): 14–36, 1991.

Ghitza, Oded. On the upper cutoff frequency of the auditory critical-band envelope detectors in the context of speech perception. The Journal of the Acoustical Society of America, 110 (3): 1628–1640, 2001.

Gilbert, Gaëtan and Lorenzi, Christian. The ability of listeners to use recovered envelope cues from speech fine structure. The Journal of the Acoustical Society of America, 119 (4): 2438–2444, 2006.

Goldstein, J. L. Auditory spectral filtering and monaural phase perception. The Journal of the Acoustical Society of America, 41 (2): 458–479, 1967b.

Goodman, Joseph W. Introduction to Fourier Optics. W. H. Freeman and Company, New York, NY, 4th edition, 2017.

Greenberg, Steven, Arai, Takayuki, and Silipo, Rosaria. Speech intelligibility derived from exceedingly sparse spectral information. In Fifth International Conference on Spoken Language Processing, Sydney, 1998.

Greenberg, Steven and Arai, Takayuki. The relation between speech intelligibility and the complex modulation spectrum. In Proc. 7th European Conference on Speech Communication and Technology (Eurospeech 2001), pages 473–476, 2001.

Hahn, Stefan L. On the uniqueness of the definition of the amplitude and phase of the analytic signal. Signal Processing, 83 (8): 1815–1820, 2003.

He, Ning-ji, Mills, John H, and Dubno, Judy R. Frequency modulation detection: Effects of age, psychophysical method, and modulation waveform. The Journal of the Acoustical Society of America, 122 (1): 467–477, 2007.

Heinz, Michael G and Swaminathan, Jayaganesh. Quantifying envelope and fine-structure coding in auditory nerve responses to chimaeric speech. Journal of the Association for Research in Otolaryngology, 10 (3): 407–423, 2009.

Heisenberg, W. Über den anschaulichen inhalt der quantentheoretischen kinematik und mechanik. Zeitschrift fur Physik, 43 (3-4): 172–198, 1927.

Helmholtz, von Hermann. The sensations of tone: As a physiological basis for the theory of music. Peter Smith, New York, NY, 6th ed. edition, 1948. Translated by Alexander J Ellis, from the 4th German edition, 1885. First published in 1863.

Hoppensteadt, Frank C and Izhikevich, Eugene M. Thalamo-cortical interactions modeled by weakly connected oscillators: Could the brain use fm radio principles? Biosystems, 48 (1-3): 85–94, 1998.

Houtgast, T and Steeneken, H JM. The modulation transfer function in room acoustics as a predictor of speech intelligibility. Acta Acustica united with Acustica, 28 (1): 66–73, 1973.

Houtgast, Tammo and Steeneken, Herman JM. A review of the mtf concept in room acoustics and its use for estimating speech intelligibility in auditoria. The Journal of the Acoustical Society of America, 77 (3): 1069–1077, 1985.

Huang, Norden E, Shen, Zheng, Long, Steven R, Wu, Manli C, Shih, Hsing H, Zheng, Quanan, Yen, Nai-Chyuan, Tung, Chi Chao, and Liu, Henry H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London A, 454 (1971): 903–995, 1998.

Huang, Norden E, Wu, Zhaohua, Long, Steven R, Arnold, Kenneth C, Chen, Xianyao, and Blank, Karin. On instantaneous frequency. Advances in Adaptive Data Analysis, 1 (02): 177–229, 2009.

Hunt, Frederick Vinton. Origins in acoustics. Acoustical Society of America, Woodbury, NY, 1992.

Iwamiya, Shin-ichiro, Nishikawa, Shinji, and Kitamura, Otoichi. Perceived principal pitch of fm-am tones when the phase difference between frequency modulation and amplitude modulation is in-phase and anti-phase. Journal of the Acoustical Society of Japan (E), 5 (2): 59–69, 1984.

Jepsen, Morten L, Ewert, Stephan D, and Dau, Torsten. A computational model of human auditory signal processing and perception. The Journal of the Acoustical Society of America, 124 (1): 422–438, 2008.

Joris, PX, Schreiner, CE, and Rees, A. Neural processing of amplitude-modulated sounds. Physiological Reviews, 84 (2): 541–577, 2004.

Kale, Sushrut, Micheyl, Christophe, and Heinz, Michael G. Implications of within-fiber temporal coding for perceptual studies of f0 discrimination and discrimination of harmonic and inharmonic tone complexes. Journal of the Association for Research in Otolaryngology, 15 (3): 465–482, 2014.

Kay, RH. Hearing of modulation in sounds. Physiological reviews, 62 (3): 894–975, 1982.

Khanna, SM and Teich, MC. Spectral characteristics of the responses of primary auditory-nerve fibers to amplitude-modulated signals. Hearing Research, 39 (1-2): 143–157, 1989a.

Khanna, SM and Teich, MC. Spectral characteristics of the responses of primary auditory-nerve fibers to frequency-modulated signals. Hearing Research, 39 (1-2): 159–175, 1989b.

Khanna, SM and Hao, LF. Nonlinear vibrations in the apex of guinea-pig cochlea. International Journal of Solids and Structures, 38 (10-13): 1919–1933, 2001.

Khanna, SM. Non-linear response to amplitude-modulated waves in the apical turn of the guinea pig cochlea. Hearing Research, 174 (1-2): 107–123, 2002.

King, Andrew, Varnet, Léo, and Lorenzi, Christian. Accounting for masking of frequency modulation by amplitude modulation with the modulation filter-bank concept. The Journal of the Acoustical Society of America, 145 (4): 2277–2293, 2019.

Klug, Achim and Grothe, Benedikt. Ethological stimuli. In Rees, Adrian and Palmer, Alan R, editors, The Oxford Handbook of Auditory Science: The Auditory Brain, volume 2, pages 173–192. Oxford University Press, New York, USA, 2010.

Koch, Ursula and Grothe, Benedikt. GABAergic and glycinergic inhibition sharpens tuning for frequency modulations in the inferior colliculus of the big brown bat. Journal of Neurophysiology, 80 (1): 71–82, 1998.

Koenig, W, Dunn, HK, and Lacy, LY. The sound spectrograph. The Journal of the Acoustical Society of America, 18 (1): 19–49, 1946.

Kragh, Helge. Magic number: A partial history of the fine-structure constant. Archive for History of Exact Sciences, 57 (5): 395–431, 2003.

Kuttruff, Heinrich. Room acoustics. CRC Group, Taylor & Francis, Boca Raton, FL, 6th edition, 2017.

Lachaux, Jean-Philippe, Rodriguez, Eugenio, Martinerie, Jacques, and Varela, Francisco J. Measuring phase synchrony in brain signals. Human Brain Mapping, 8 (4): 194–208, 1999.

Laitinen, Mikko-Ville, Disch, Sascha, and Pulkki, Ville. Sensitivity of human hearing to changes in phase spectrum. Journal of the Audio Engineering Society, 61 (11): 860–877, 2013.

Langner, Gerald. Neural processing and representation of periodicity pitch. Acta Oto-Laryngologica, 117 (sup532): 68–76, 1997.

Lentz, Jennifer J and Valentine, Susie. Across-frequency processing of modulation phase differences in hearing-impaired listeners. The Journal of the Acoustical Society of America, 138 (3): EL205–EL211, 2015.

Lepage, Kyle Q and Vijayan, Sujith. The relationship between coherence and the phase-locking value. Journal of Theoretical Biology, 435: 106–109, 2017.

Licklider, Joseph CR. On the process of speech perception. The Journal of the Acoustical Society of America, 24 (6): 590–594, 1952.

Lorenzi, Christian, Gilbert, Gaëtan, Carn, Héloïse, Garnier, Stéphane, and Moore, Brian CJ. Speech perception problems of the hearing impaired reflect inability to use temporal fine structure. Proceedings of the National Academy of Sciences, 103 (49): 18866–18869, 2006.

Loughlin, Patrick J and Tacer, Berkant. On the amplitude-and frequency-modulation decomposition of signals. The Journal of the Acoustical Society of America, 100 (3): 1594–1601, 1996.

Mandel, L. Complex representation of optical fields in coherence theory. Journal of the Optical Society of America, 57 (5): 613–617, 1967.

Mandel, Leonard and Wolf, Emil. Optical Coherence and Quantum Optics. Cambridge University Press, Cambridge, United Kingdom, 1995.

Mayer, Alfred M. Art XXI. Researches in acoustics, Paper No. 6. American Journal of Science and Arts, Third Series, 8 (46): 241–255, 1874.

Moore, Brian CJ and Glasberg, Brian R. Formulae describing frequency selectivity as a function of frequency and level, and their use in calculating excitation patterns. Hearing Research, 28 (2-3): 209–225, 1987.

Moore, Brian CJ, Glasberg, Brian R, and Schooneveldt, Gregory P. Across-channel masking and comodulation masking release. The Journal of the Acoustical Society of America, 87 (4): 1683–1694, 1990.

Moore, Brian CJ. Interference effects and phase sensitivity in hearing. Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 360 (1794): 833–858, 2002.

Moore, Brian CJ. The role of temporal fine structure processing in pitch perception, masking, and speech perception for normal-hearing and hearing-impaired people. Journal of the Association for Research in Otolaryngology, 9 (4): 399–406, 2008.

Moore, Brian CJ. An introduction to the psychology of hearing. Brill, Leiden, Boston, 6th edition, 2013.

Moore, Brian CJ. Auditory processing of temporal fine structure: Effects of age and hearing loss. World Scientific Publishing Co. Pte. Ltd., Singapore, 2014.

Moore, Brian CJ. The roles of temporal envelope and fine structure information in auditory perception. Acoustical Science and Technology, 40 (2): 61–83, 2019.

Moore, Brian CJ, Glasberg, Brian R, Gaunt, Tracey, and Child, Tim. Across-channel masking of changes in modulation depth for amplitude-and frequency-modulated signals. The Quarterly Journal of Experimental Psychology, 43 (3): 327–347, 1991.

Moore, Brian CJ and Sek, Aleksander. Discrimination of modulation type (amplitude modulation or frequency modulation) with and without background noise. The Journal of the Acoustical Society of America, 96 (2): 726–732, 1994a.

Moore, Brian CJ and Sek, Aleksander. Effects of carrier frequency and background noise on the detection of mixed modulation. The Journal of the Acoustical Society of America, 96 (2): 741–751, 1994b.

Moore, Brian CJ and Sek, Aleksander. Effects of carrier frequency, modulation rate, and modulation waveform on the detection of modulation and the discrimination of modulation type (amplitude modulation versus frequency modulation). The Journal of the Acoustical Society of America, 97 (4): 2468–2478, 1995.

Moore, Brian CJ and Sek, Aleksander. Detection of frequency modulation at low modulation rates: Evidence for a mechanism based on phase locking. The Journal of the Acoustical Society of America, 100 (4): 2320–2331, 1996.

Moore, Brian CJ and Sek, Aleksander. Effects of relative phase and frequency spacing on the detection of three-component amplitude modulation. The Journal of the Acoustical Society of America, 108 (5): 2337–2344, 2000.

Moore, Brian CJ and Skrodzka, Ewa. Detection of frequency modulation by hearing-impaired listeners: Effects of carrier frequency, modulation rate, and added amplitude modulation. The Journal of the Acoustical Society of America, 111 (1): 327–335, 2002.

Mowlaee, Pejman, Saeidi, Rahim, and Stylianou, Yannis. Advances in phase-aware signal processing in speech communication. Speech Communication, 81: 1–29, 2016.

Nábělek, Igor V. Temporal summation of constant and gliding tones at masked auditory threshold. The Journal of the Acoustical Society of America, 64 (3): 751–763, 1978.

Nelson, PG, Erulkar, SD, and Bryan, JS. Responses of units of the inferior colliculus to time-varying acoustic stimuli. Journal of Neurophysiology, 29 (5): 834–860, 1966.

Ni, Xuelei Sherry and Huo, Xiaoming. Statistical interpretation of the importance of phase information in signal and image reconstruction. Statistics & Probability Letters, 77 (4): 447–454, 2007.

Nussenzveig, Herch Moyses. Causality and dispersion relations. Academic Press, Inc., New York, NY, 1972.

Nuttall, Alfred L, Ricci, Anthony J, Burwood, George, Harte, James M, Stenfelt, Stefan, Cayé-Thomasen, Per, Ren, Tianying, Ramamoorthy, Sripriya, Zhang, Yuan, Wilson, Teresa, Lunner, Thomas, Moore, Brian C. J., and Fridberger, Anders. A mechanoelectrical mechanism for detection of sound envelopes in the hearing organ. Nature Communications, 9 (1): 1–11, 2018.

Oppenheim, Alan V and Lim, Jae S. The importance of phase in signals. Proceedings of the IEEE, 69 (5): 529–541, 1981.

Otsuka, Sho and Furukawa, Shigeto. Conversion of amplitude modulation to phase modulation in the human cochlea. Hearing Research, page 108274, 2021.

Palmer, Alan Richard. Encoding of rapid amplitude fluctuations by cochlear-nerve fibres in the guinea-pig. Archives of Oto-Rhino-Laryngology, 236 (2): 197–202, 1982.

Paraouty, Nihaad, Stasiak, Arkadiusz, Lorenzi, Christian, Varnet, Léo, and Winter, Ian M. Dual coding of frequency modulation in the ventral cochlear nucleus. Journal of Neuroscience, 38 (17): 4123–4137, 2018.

Patterson, Roy D. A pulse ribbon model of monaural phase perception. The Journal of the Acoustical Society of America, 82 (5): 1560–1586, 1987.

Picinbono, Bernard. On instantaneous amplitude and phase of signals. IEEE Transactions on Signal Processing, 45 (3): 552–560, 1997.

Plomp, Reinier and Steeneken, Herman JM. Effect of phase on the timbre of complex tones. The Journal of the Acoustical Society of America, 46 (2B): 409–421, 1969.

Potter, Ralph Kimball. Visible patterns of sound. Science, 102 (2654): 463–470, 1945.

Potter, Ralph K and Steinberg, John C. Toward the specification of speech. The Journal of the Acoustical Society of America, 22 (6): 807–820, 1950.

Qasim, Salman E, Fried, Itzhak, and Jacobs, Joshua. Phase precession in the human hippocampus and entorhinal cortex. Cell, 184 (12): 3242–3255, 2021.

Riesz, RR. Differential intensity sensitivity of the ear for pure tones. Physical Review, 31 (5): 867, 1928.

Rihaczek, AW and Bedrosian, E. Hilbert transforms and the complex representation of real signals. Proceedings of the IEEE, 54 (3): 434–435, 1966.

Rosen, Stuart. Temporal information in speech: Acoustic, auditory and linguistic aspects. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences, 336 (1278): 367–373, 1992.

Saberi, Kourosh and Haftert, Ervin R. A common neural code for frequency-and amplitude-modulated sounds. Nature, 374 (6522): 537–539, 1995.

Schimmel, Steven and Atlas, Les. Coherent envelope detection for modulation filtering of speech. In IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), 2005, volume 1, pages I–221–I–224. IEEE, 2005.

Schreiner, Christoph E and Langner, Gerald. Periodicity coding in the inferior colliculus of the cat. II. Topographical organization. Journal of Neurophysiology, 60 (6): 1823–1840, 1988.

Shannon, Robert V, Zeng, Fan-Gang, Kamath, Vivek, Wygonski, John, and Ekelid, Michael. Speech recognition with primarily temporal cues. Science, 270 (5234): 303–304, 1995.

Sheft, Stanley, Ardoint, Marine, and Lorenzi, Christian. Speech identification based on temporal fine structure cues. The Journal of the Acoustical Society of America, 124 (1): 562–575, 2008.

Shekel, J. Instantaneous frequency. Proceedings of the Institute of Radio Engineers, 41 (4): 548–548, 1953.

Shower, EG and Biddulph, Rulon. Differential pitch sensitivity of the ear. The Journal of the Acoustical Society of America, 3 (2A): 275–287, 1931.

Sinex, Donal G and Geisler, C Daniel. Auditory-nerve fiber responses to frequency-modulated tones. Hearing Research, 4 (2): 127–148, 1981.

Smith, Zachary M, Delgutte, Bertrand, and Oxenham, Andrew J. Chimaeric sounds reveal dichotomies in auditory perception. Nature, 416 (6876): 87–90, 2002.

Srinath, Ramanujan and Ray, Supratim. Effect of amplitude correlations on coherence in the local field potential. Journal of Neurophysiology, 112 (4): 741–751, 2014.

Strickland, Elizabeth A, Viemeister, Neal F, Fantini, Deborah A, and Garrison, Margery A. Within-versus cross-channel mechanisms in detection of envelope phase disparity. The Journal of the Acoustical Society of America, 86 (6): 2160–2166, 1989.

Taylor, James D. Introduction to Ultra-Wideband Radar Systems. CRC Press, Boca Raton, FL, 1995.

Teager, HM and Teager, SM. Evidence for nonlinear sound production mechanisms in the vocal tract. In Hardcastte, W. J. and Marchat, A., editors, Speech Production and Speech Modelling, pages 241–261. Kluwer Academic Publishers, NL, 1990.

Theunissen, Frédéric and Miller, John P. Temporal encoding in nervous systems: A rigorous definition. Journal of Computational Neuroscience, 2 (2): 149–162, 1995.

Thompson, Peter M. Snap, crackle, and pop. In Proceedings of AIAA Southern California Aerospace Systems and Technology Conference, 2011.

Thoret, Etienne, Ystad, Sølvi, and Kronland-Martinet, Richard. Hearing as adaptive cascaded envelope interpolation. Communications Biology, 6 (1): 671, 2023.

Tiffin, Joseph. Some aspects of the psychophysics of the vibrato. Psychological Monographs, 41 (4): 153, 1931.

Turner, R Steven. The Ohm-Seebeck dispute, Hermann von Helmholtz, and the origins of physiological acoustics. The British Journal for the History of Science, 10 (1): 1–24, 1977.

Vakman, David. On the analytic signal, the Teager-Kaiser energy algorithm, and other methods for defining amplitude and frequency. IEEE Transactions on Signal Processing, 44 (4): 791–797, 1996.

Vater, Marianne. Single unit responses in cochlear nucleus of horseshoe bats to sinusoidal frequency and amplitude modulated signals. Journal of Comparative Physiology, 149 (3): 369–388, 1982.

Viemeister, Neal F. Temporal modulation transfer functions for audition. The Journal of the Acoustical Society of America, 53 (1): 312–312, 1973.

Viemeister, Neal F. Temporal modulation transfer functions based upon modulation thresholds. The Journal of the Acoustical Society of America, 66 (5): 1364–1380, 1979.

Voelcker, Herbert B. Toward a unified theory of modulation part I: Phase-envelope relationships. Proceedings of the IEEE, 54 (3): 340–353, 1966.

Wever, Ernest Glen. Theory of Hearing. John Wiley & Sons New York, Chapman & Hall Limited, London, 1949.

Wheeler, HA. The solution of unsymmetrical-sideband problems with the aid of the zero-frequency carrier. Proceedings of the IRE, 29 (8): 446–458, 1941.

Whiteford, Kelly L and Oxenham, Andrew J. Sensitivity to frequency modulation is limited centrally. Journal of Neuroscience, 43 (20): 3687–3695, 2023.

Whitfield, Ian Cunliffe. The electrical responses of the unanaesthetised auditory cortex in the intact cat. Electroencephalography and Clinical Neurophysiology, 9 (1): 35–42, 1957.

Whitfield, IC and Evans, EF. Responses of auditory cortical neurons to stimuli of changing frequency. Journal of Neurophysiology, 28 (4): 655–672, 1965.

Xu, Li and Pfingst, Bryan E. Relative importance of temporal envelope and fine structure in lexical-tone perception (L). The Journal of the Acoustical Society of America, 114 (6): 3024–3027, 2003.

Yao, Jianping, Zeng, Fei, and Wang, Qing. Photonic generation of ultrawideband signals. Journal of Lightwave Technology, 25 (11): 3219–3235, 2007.

Yost, William A and Sheft, Stanley. Across-critical-band processing of amplitude-modulated tones. The Journal of the Acoustical Society of America, 85 (2): 848–857, 1989.

Yue, Qi, Casseday, John H, and Covey, Ellen. Response properties and location of neurons selective for sinusoidal frequency modulations in the inferior colliculus of the big brown bat. Journal of Neurophysiology, 98 (3): 1364–1373, 2007.

Zeng, Fan-Gang, Nie, Kaibao, Stickney, Ginger S, Kong, Ying-Yee, Vongphoe, Michael, Bhargave, Ashish, Wei, Chaogang, and Cao, Keli. Speech recognition with amplitude and frequency modulations. Proceedings of the National Academy of Sciences, 102 (7): 2293–2298, 2005.

Zweig, George, Lipes, R, and Pierce, JR. The cochlear compromise. The Journal of the Acoustical Society of America, 59 (4): 975–982, 1976.

Zwicker, E. Die grenzen der Hörbarkeit der Amplitudenmodulation und der Frequenz-modulation eines Tones. Acta Acustica united With Acustica, 2 (3): 125–133, 1952.

Zwicker, Eberhard. Die elementaren Grundlagen zur Bestimmung der Informationskapazität des Gehörs. Acta Acustica united with Acustica, 6 (4): 365–381, 1956.

Zwicker, Eberhard, Flottorp, Georg, and Stevens, Stanley Smith. Critical band width in loudness summation. The Journal of the Acoustical Society of America, 29 (5): 548–557, 1957.