Chapter 5
Three approaches to information transfer
5.1 Introduction
Information theory, communication theory, and imaging optics all deal with information transfer using different but complementary paradigms. Information theory deals with abstract and probability-based information transfer between a source and a receiver through a noisy communication channel, and how coding can be used to optimize the communication. Communication theory offers mathematical tools that prescribe how information transfer can be achieved in practice, by considering real physical signals, which can be applied in hardware and in software. Optical imaging specifically deals with the transfer of the information contained in spatial objects, most conventionally by means of quadratic transformations that represent how light waves propagate in space. All three theories complement one another in different ways, and while they are occasionally packaged into common applications, they are usually studied separately.
While by no means foreign to hearing science, the three theories had arguably little direct influence on its progress and are nowhere considered “staple” disciplines for hearing. However, several concepts from each field were imported into hearing and are occasionally used without disclosing their parent discipline, which runs the risk of losing the grounding and intuition that can be garnered by having the full context.
The goal of this chapter is to show how some of the basic paradigms of information, communication, and imaging theories overlap. Some of the most useful concepts in information theory are presented in a short overview and several historical connections with auditory research are highlighted. Then, the general communication system is presented as a practical realization of the ideal one described in information theory. It will be argued in broad strokes that hearing can be readily fitted into a communication system paradigm. We also discuss the various similarities and differences between the general communication system and a generic single-lens imaging system. The perspectives offered in the following sections are intended to bolster our confidence in borrowing from the rich methods that have been developed in communication and imaging theories. Still, the knowledge about these theories that will be required later in this work is relatively limited. Hence, the review of these theories is brief and qualitative and is mainly geared to familiarize the reader with basic concepts. Showing that hearing can be also recast as an imaging system will be the subject of later chapters in this work.
As in other introductory chapters, the material presented in the following sections may appear trivial to communication or electronic engineers and to people with similar backgrounds. However, the connections to hearing and the interrelationship between the three approaches to information transfer have not been previously presented in the context of hearing or acoustics, to the best knowledge of the author.
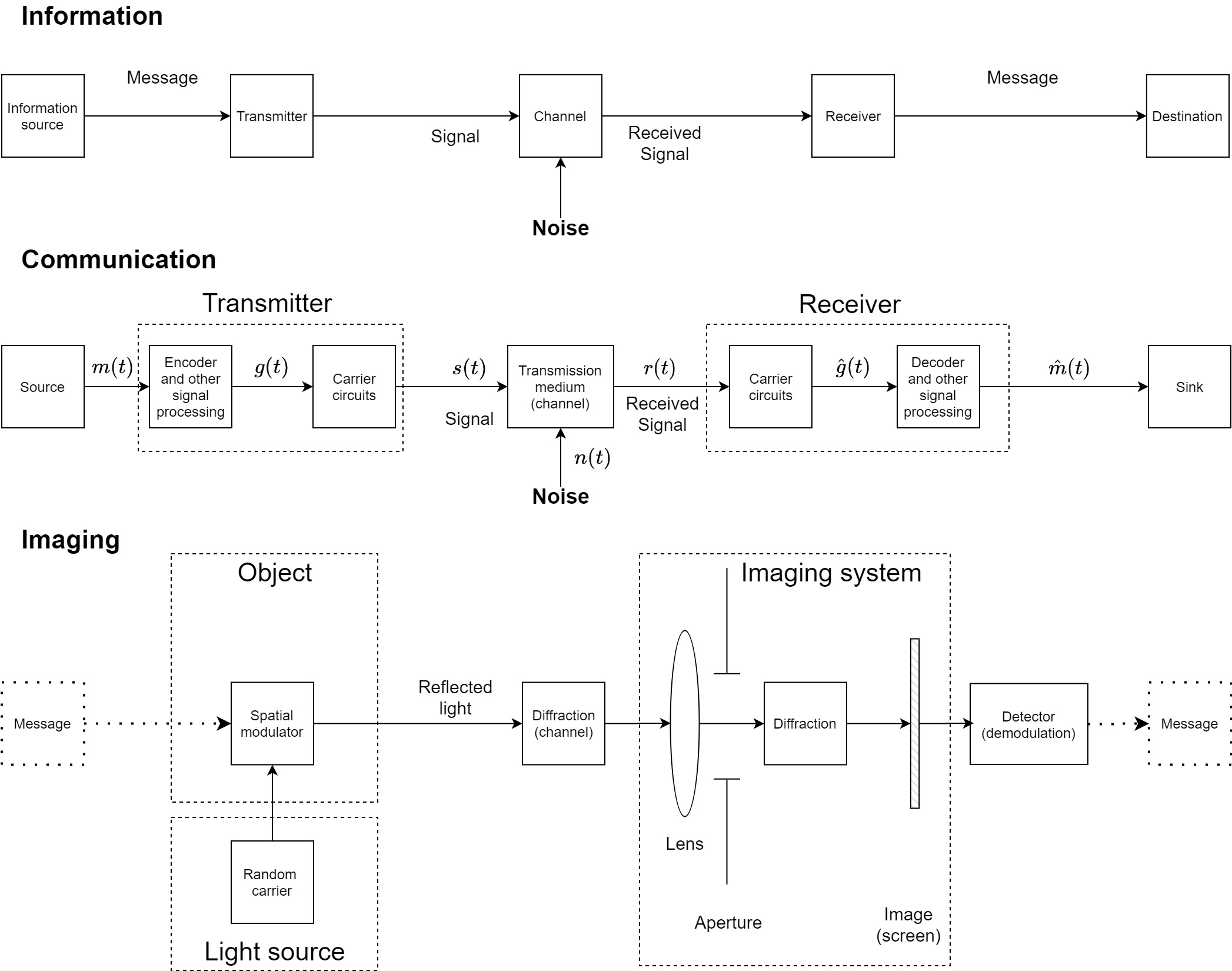
Figure 5.1: The three basic paradigms of information theory, communication theory, and optical imaging. The upper diagram is a reproduction of Figure 1 in Shannon (1948). The middle diagram is a reproduction of Figure 1-1 in Couch II (2013). The dotted lines in the imaging system around the message on the source and destination ends imply that information transfer in imaging is optional.
5.2 Information
The term information is used differently in lay language and in the branch of mathematics known as information theory. In common usage, it is typical to attribute information to facts and data that convey meaning to people, whereas in information theory it is none of these things. Even when used in other branches of science, the term is often applied quite intuitively and non-technically, which tends to make the initial encounter with the formal and abstract nature of information within information theory quite overwhelming for newcomers. Nevertheless, the impact of information theory on modern science and technology cannot be overstated. Still, there have been several ongoing important controversies that are more philosophical in nature, regarding the true nature of information, such as its applicability to systems that are not probabilistically and symbolically closed, and to its complete disallowance of meaning to have anything to do with the theory.
While several theories of information have been proposed over the past century, Claude Shannon's information theory rules supreme (Shannon, 1948). His seminal article, originally targeting the problem of communication, is self-contained and provides most of the insight needed for familiarization with the basic concepts. Despite its highly mathematical nature, information theory has several general results that are qualitatively useful for this work, although usually indirectly, so the overview below is very concise. Interested readers can find out more from Shannon's original paper (also in the edition with Weaver's introduction, Shannon and Weaver, 1949) and many introductory texts at different levels of abstraction and rigor (e.g., Pierce, 1980; Cover and Thomas, 2006; Ben-Naim, 2008).
5.2.1 Information theory in a nutshell
Discrete communication
Shannon analyzed the transfer of information within a communication system that consists of an information source that sends a message through a transmitter, a channel, and a receiver, to the information destination (top diagram in Figure 5.1). The content of the message is immaterial for the analysis—only the relative probability in which it appears out of the ensemble of all possible messages that can be sent over the channel. Thus, the messages are defined with respect to a closed-set of symbols that are commonly shared by the transmitter and receiver (sometimes called an alphabet). Each symbol can appear in communication at a certain probability and be part of a sequence of symbols that forms the message. The lower the likelihood of a symbol to appear, the more information it carries. In contrast, the more predictable a symbol is, the less information it carries. Therefore, according to this definition the amount of information relates to the ability of a given message to remove uncertainty from the communication.
The simplest communication system consists of only two symbols, such as “yes” and “no”, or 0 and 1. More complex messages can always be expressed as sequences of 0s and 1s (or answers to yes/no questions), without the loss of generality. By stating a few very basic requirements, Shannon was able to arrive at a unique measure of information, which he called entropy (borrowing from statistical mechanics, see §5.2.2)
| \[ H = -\sum_{n=1}^N p_i \log_2{p_i} \] | (5.1) |
where \(H\) is the entropy (or Shannon's entropy) that is computed over the probability mass function \(p\), which is defined over a set of \(N\) symbols (symbols with probability 0 are defined to have a corresponding zero entropy). For a two-symbol communication, if the two symbols appear at equal probability, then their entropy is \(H=1\), so that each message is said to carry on average one bit of information45.
It should be underlined that because messages are modeled as if drawn from a specific probability distribution, the entropy carried by a single message can only be understood as an element of an ensemble. Therefore, it is not meaningful to think of a standalone message that is being communicated if it is not embedded in a statistical relationship that exists within the full communication system.
The channel in information theory is also defined probabilistically. In noise-free communication, the message that is transmitted is received unchanged. In the presence of noise, the likelihood for communication errors increases, which means that the wrong symbol can be received compared to what was sent. Errors create overall ambiguity in the message reception. Because of noise, channels are physically limited in their channel capacity, which is the maximum amount of information (or number of symbols) that can be transmitted in the channel per unit time and cannot exceed the information rate of the source46. If a higher rate than the channel capacity is transmitted, then it is certain that there will be errors in reception. However, it is theoretically possible to communicate information with an arbitrarily low error rate within the channel capacity. Achieving a low error rate requires coding of the messages.
It is possible to reframe the coupling between any two physical systems as a channel, if we retain the abstract mathematical point of view. Hence, channels are not realized only in the form of cables or wireless transmission. Accordingly, the start and end points of communication may be somewhat arbitrary and can depend on the desired analysis. However, according to the data-processing inequality, information that passes through a cascade of channels can remain at most equal to the amount of information in the original message, or get gradually lost between channels—a gain of information down the communication chain is impossible (Cover and Thomas, 2006; pp. 34–35).
Coding entails a transformation to the message representation that does not change its contents and its source entropy, but impacts its length. If the coded message contains predictable elements—for example, when a symbol identity can be confidently guessed by the identity of the previous two symbols—then it is said to have a redundancy. For example, in the statement “the integer between 1 and 3 is 2”, the “is 2” can be considered redundant. There is flexibility in designing codes that serve different purposes—either to enhance redundancies, or eliminate them using (lossless) compression. Adding redundancies serves to optimize the communication robustness to errors (noise), as they can facilitate error correction, whereby the redundant information can be used to ensure the veracity of the message. In contrast, compression increases the transmission economy by employing a minimal number of symbols to communicate a particular message. In practice, a minimal error rate has to be tolerated, which means that some of the information from the source becomes lost in transmission. Alternatively, limitations on the maximum rate may exist, which force the communication system designer to exclude some information from the coded messages through lossy compression.
Continuous communication
The description above applies to discrete messaging systems, in which the symbols are fixed. Information theory can be applied to continuous systems as well—something which introduces additional challenges to communication and to its mathematical representation. The same relations apply using probability density functions and integrals instead of probability mass functions and sums. Strictly speaking, continuous signals contain an infinite amount of information because it is always possible to represent a real continuous quantity with increased precision that requires more bits of information (e.g., to represent a real number with more digits after the decimal point). Thus, continuous entropy is defined as a relative measure and requires a reference level to enable its calculation.
In practice, continuous information is often manipulated by discretization—by sampling the signal in time and by quantizing its level. The number of bits allocated to each quantized sample depends on the available dynamic range in the system. The larger the dynamic range, the higher is the attainable fidelity of the quantized signal, which can be measured in number of bits per sample. The channel capacity is a function of the signal-to-noise ratio (SNR)
| \[ C = B\log_2 \left( 1+ \frac{S}{N} \right) \] | (5.2) |
in which \(B\) is the bandwidth, \(S\) is the power in the signal and \(N\) is the power of the noise. Higher channel capacity, measured in bits per second, can be obtained with higher SNR.
A complete equivalence can be drawn between discrete and continuous communication through sampling the analog signal. The sampling process transforms a bandlimited signal of bandwidth \(B\) to a sequence of discrete samples. These samples can be used to mathematically reconstruct the original signal perfectly, as long as the signal is sampled with at least twice the bandwidth of the highest frequency component in the bandlimited signal, according to the sampling theorem (Nyquist, 1928; Shannon, 1948)47
| \[ f_s \geq 2B \] | (5.3) |
where \(f_s\) is the sampling rate or sampling frequency. The bound that is achieved when \(f_s=2B\) is called the Nyquist rate (or Nyquist frequency). When a signal is regularly sampled below the Nyquist rate, the reconstructed signal may be distorted due to aliasing. This is caused when frequency components in the passband \(f>f_s/2\) are wrongly reproduced as folded components within the new passband range (e.g., at \(f_s/2-f\)) (see also §14.3 and Figure §E.3).
The source entropy is maximal when all symbols can appear at equal probabilities. This is equivalent to saying that the message symbols are completely random and no additional information is available that can reduce the length of the message that has to be communicated. The continuous analog distribution that maximizes the entropy of the channel is the Gaussian distribution, or white noise.
5.2.2 The physicality of information
The abstract nature of information as was defined by Shannon—a mathematical entity that depends on the probability distributions of arbitrary symbols—should not be interpreted as though information can exist without a physical substrate. Regardless of how the information bits manifest physically in transmission, the physical parts of the communication system should be able to resolve the differences between different levels or different combinations of bits. The manifested difference between symbols may be mapped to any measurable quantity that is being transmitted in the channel such as power, frequency, or periodicity pattern, whereas higher-level symbolic representations may relate to shape, color, pitch, duration, etc. The simplest symbol set contains only two distinct states, 1 and 0, so a physical system that can represent them must have at least two stable states, which can be mapped to the two symbols (Landauer, 1961). It should be possible to change the output of the transmitter, at will, to either one of these two states. Similarly, the receiver must be capable of resolving the two states of its input stage, so they can be mapped to two different symbols.
Integrating information into theoretical physics has been fraught with controversy ever since Shannon's work and possibly even before (Szilard, 1929). One major point of contention has been Shannon's choice to name the information measure “entropy” after a quantity from statistical mechanics that has the same mathematical form. As the two quantities are derived from probability distributions, some scholars have argued that they are in fact the same, whereas others have argued that the overlap is a mere coincidence that produces incoherent interpretation. However, sidestepping the controversy, a unified concept of entropy and information has been successfully treated as a de-facto physical quantity that plays a key role in modern scientific fields such as astrophysics and quantum computing. The most embracing take was probably the one expressed by the physicist John Archibald Wheeler, who has argued that information is a fundamental property of the universe (Wheeler, 1990). Others have proven that information may be defined axiomatically, so probability can be derived from information instead of the other way round (Ingarden and Urbanik, 1962; Jumarie, 2000).
While the notion that “information is physical” (Landauer, 1996) has been one of the inspirations for the present work, the intricacies of this topic are not directly relevant to its main thread. The interested reader may consult Ben-Naim (2008) for an engrossing treatment of the relation between physics and information theory.
5.2.3 Information theory and hearing
Because of its highly general formulation, information theory seems to have been applied in almost every domain of science, but at varying degrees of rigor. Information theory has indirectly had the most impact on hearing science through its significant role in digital signal processing (by bridging analog and digital signal representations) and in audio compression technology (combining perceptual coding and data compression). Additionally, various effects in hearing were modeled with reference to information theory, but with different degrees of adherence to the mathematical theory of information. Undoubtedly, cognitive psychology and neuroscience are where it has resonated the most as it seems that “information processing” is a given in brain circuits that relate to cognition.
An early and influential adoption of key concepts such as information bit and channel capacity can be seen in early cognitive psychology (along with computation theory), which tended to apply it in a more metaphorical way that did not always cite Shannon's work directly (e.g., Miller, 1956; Chomsky, 1956; Broadbent, 1958/1966; Kahneman, 1973). Side by side, information theory conceptually inspired several seminal psychoacoustical papers that introduced ideas such as the redundancy in speech (Miller and Licklider, 1950), confusion matrices in speech reception (Miller and Nicely, 1955), the cocktail party effect (James, 1890; p. 420) representing limited attentional and auditory channel capacity (Cherry, 1953), and lipreading as a parallel information channel to acoustic speech (Sumby and Pollack, 1954). Typically, these studies selected the parts of speech that should be treated as the information to be quantified, which is convenient symbolically, but cannot be easily generalized to other signals. An early estimate of a general auditory channel capacity in bits per second was attempted by Jacobson (1950), Jacobson (1951b).
In neuroscience, Edgar Adrian used terminology that borrowed from early communication theory that predated information theory (Garson, 2015). Even much later, neuroscience still held on to a conceptualization of neural coding and information processing that is independent of the information theoretical concepts that bear the same names (Perkel and Bullock, 1968). However, some ideas about neural coding have clearly been influenced by information theory. Perhaps the most famous example is the efficient coding hypothesis, which states that as sensory information is processed in more central areas, the brain gradually eliminates redundant information that is a characteristic of natural signals (Attneave, 1954; Barlow, 1961). More rigorous usage of information theory has become more prevalent in neuroscience in the last decades (Rieke et al., 1999) and, gradually, in auditory neuroscience (e.g., Chechik et al., 2006; Nelken and Chechik, 2007) and speech perception (Gwilliams and Davis, 2022).
There has been an ongoing controversy about the usefulness and validity of implementing information theoretic concepts both in cognitive psychology and in neuroscience, as well as in other sciences, which Shannon himself warned against (Shannon, 1956). For example, to Neisser (2014, pp. 7–8), information processing was the essential variable of cognitive psychology—“Information is what is transformed, and the structured pattern of its transformations is what we want to understand”—yet he considered the quantitative measures of information theory overall unfruitful in psychology (unlike computation theory that has led to more insights). Another criticism about the use of information theory in psychology is the indiscriminate reliance on statistics, which suggests that sequences of events (e.g., sensory inputs) exist only as probabilistic entities, whereas in reality they are rarely random and can be significant to the person (Luce, 2003). Similarly, in neuroscience, Brette (2019) contended that the popular concept of neural coding contains the conditions and context that are specific to the experimental setting. He argued that coding should be instead taken only metaphorically, if neural patterns are to be modeled with information theoretical tools. Information theory itself may be deficient in explanatory power, as it does not provide meaning to the coded sequences, which have to be sought externally. Another recent critique has pointed to that the neuroscientific literature often neglects to identify the different parts of the communication system, like source, channel, and receiver within the brain or the external environment, which results in incoherent modeling (Nizami, 2019).
5.2.4 Auditory information
In the context of the present work, it is the acoustically transmitted information that is being tracked from the object to the brain. It is explicitly assumed that however the information is physically expressed in the signal domain, it is largely conserved throughout the various transformations that the signal undergoes: from acoustical waves in air or water, through to the outer ear waveguide, elastic vibrations of the eardrum, mechanical motion of the stapes, compression waves in the cochlea, elastic traveling wave of the basilar membrane, hair-cell deflection, mechanoelectric transduction, and neural spikes. The most critical stage is the final transduction between the fluid motion in the inner ear and the neural domain, in which the carrier energy and form are markedly changed from the mechanical waves, and where information processing conventionally begins (i.e., according to neuroscience and cognitive psychology). An implicit information conservation assumption has been repeatedly made in numerous other models of the auditory system, which apply a continuous signal processing, energetic, or phenomenological analysis between the cochlear and neural parts of the auditory system. Arguably, such an assumption is necessary to meaningfully interpret the function of any sensory systems—hearing being no exception. A reinterpretation of various auditory mechanisms was presented in Weisser (2019); Weisser (2018, pp. 123–162), where it was contended that cumulative information loss is a unifying principle of auditory perception, which is necessary to avoid perceptual and cognitive overload.
As will be seen below, communication theory introduces additional layers of signal processing that bring Shannon's stripped-down communication system a few steps closer to physical realization. In visual and auditory sensation, the communication system parts are relatively unambiguous, which either obviates or defers the discussion about meaning and coding and pushes it further downstream in the brain processing. In a sense, we will be taking Luce (2003) up on his (somewhat overstated) observation: “The elements of choice in information theory are absolutely neutral and lack any internal structure; the probabilities are on a pure, unstructured set whose elements are functionally interchangeable. That is fine for a communication engineer who is totally unconcerned with the signals communicated over a transmission link; interchanging the encoding matters not at all.” Therefore, we shall shift our attention to communication theory in the following discussion.
5.3 Communication
Communication theory and engineering historically preceded information theory, but are a logical and technical elaboration of its principles. Here, the communication process is physical and no longer abstract. The reach of communication theory within hearing science is found in the methods and jargon that have entered the field. Any mention of amplitude-, phase-, or frequency-modulation, envelope, carrier, and instantaneous amplitude, phase, and frequency owes something to communication theory. Half-wave rectification that is commonly attributed to the inner hair cell transduction operation is also a common building block that is used in communication demodulation. While these terms are routinely found in other disciplines as well, they are most instrumental in communication technology. It is worth noting that acoustic devices that rely on the same communication-theoretic principles as have been established for electromagnetic waves has found increasing use in underwater applications, most notably in acoustic modems and telemetry (e.g., Stojanovic et al., 1993; Sendra et al., 2015).
There is a wealth of literature on communication theory. The brief overview below is mostly based on Couch II (2013) with some input from Middleton (1996), Proakis and Salehi (2014), and Ling (2017).
5.3.1 Communication theory basics
All communication systems consist of a transmitter, a channel, and a receiver (middle diagram in Figure 5.1). The system is capable of transmitting low-frequency messages from an information source to a remote destination. The information may be either analog or digital, in which case several steps of encoding are included in the process. The information is fed into the transmitter, which processes the messages and up-converts the resultant signal to a suitable frequency for transmission (always as an analog signal). Mathematically, it is done by modulating the low-frequency baseband signal (that corresponds to the information) onto a high-frequency carrier, which forms the signal for bandpass communication48. The modulated carrier is amplified and transmitted into a channel—a physical medium—where the signal generally becomes attenuated and corrupted by noise through propagation. A remote receiver then down-converts the signal through demodulation to low frequency and usually performs additional signal processing to extract the baseband message, which can be read or further processed by the operator.
A plethora of signaling techniques have been developed that are widely applied in modern electronic hardware and in software. However, the basic analysis leading up to these techniques is done without considering the electronic or computational implementation, and is therefore relevant to any technology that can assume the same mathematics.
A general bandpass signal \(s(t)\) can take either one of three canonical forms. The first one is
| \[ s(t) = a(t)\cos[\omega_c t + \varphi(t)] \] | (5.4) |
where \(a(t)\) and \(\varphi(t)\) are the real, time-dependent, non-negative envelope and phase functions, respectively. Both modulate a sinusoid carrier of frequency \(\omega_c\). The signal is sometimes more conveniently expressed as a sum of two orthogonal channels of the same carrier, but \(90^\circ\) shifted
| \[ s(t) = x(t)\cos(\omega_c t) - y(t)\sin(\omega_c t) \] | (5.5) |
with the two real functions being \(x(t)\), the in-phase modulation, and \(y(t)\), the quadrature modulation associated with \(s(t)\). Another equivalent representation of the bandpass signal uses the real part of the complex signal
| \[ s(t) = \Re \left[ g(t)e^{i\omega_c t}\right] \] | (5.6) |
where \(g(t)\) is the complex envelope that is related to the previous expressions through \(g(t) = a(t)e^{i\varphi(t)}\) and also \(g(t) = x(t) + iy(t)\). The three expressions are completely general for any time signals (see §6.3 and Couch II, 2013; pp. 238–241). In the context of communication, the complex envelope is also referred to as a mapping operation of the message \(m(t)\), so that \(g(t) = g[m(t)]\).
Modulation can be applied to any of the real functions that are used in the canonical signal representations. The simplest type is amplitude modulation (AM) on \(a(t)\), but the term is also used to specifically refer to modulation of the form \(a(t) = 1 + m\cos(\omega_m t)\). Another basic type is angle modulation, which can refer directly to the phase in phase modulation (PM), or to its derivative in frequency modulation (FM). If \(x(t)\) and \(y(t)\) are modulated, then it is called quadrature modulation (QM).
According to the modulation type produced by the transmitter, the receiver has to perform an inverse demodulation operation in order to recover the baseband message. This constrains the possible modulation to relatively simple mathematical operations that are one-to-one in the frequency range of interest. There are two types of generalized transmitters, which can produce any type of signal modulation. One type is capable of producing AM and PM (top diagram of Figure 5.2) that is ideal for Eqs. 5.4 and 5.6. The second type (not shown) produces QM, which is particularly handy to use with Eq. 5.5. In this work we will focus on the complex canonical signal form (Eq. 5.6), and hence adopt the generalized transmitter of the first type.

Figure 5.2: Generalized transmitter and receiver diagrams. The receiver contains an optional intermediate-frequency stage that facilitates baseband signal processing. The local oscillator is used only in coherent detection. The diagrams are redrawn after Figures 4-27 and 4-29 in Couch II (2013)
The modulated carrier is transmitted into a communication channel—a physical medium that connects the transmitter and the receiver. In wireless communication it is usually the atmosphere, and in wired communication it is a cable or an optical fiber. When propagating in the atmosphere, the signal is attenuated and is subject to distortion from dispersion and variable atmospheric conditions. Moreover, the received signal may be the sum of several reflections (a multipath channel) that cause pulse broadening at the receiver. Additional detrimental effects of the channel are interference from other transmissions and noise (usually thermal). In general, for a linear and time-invariant channel with impulse response \(h(t)\) and noise \(n(t)\), the received signal \(r(t)\) is of the form:
| \[ r(t) = s(t)*h(t) + n(t) \] | (5.7) |
where \(*\) designates the convolution operation. The ideal communication system provides immunity to the forms of degradation encompassed by \(h(t)\), so that the receiver is able to recover the message without any errors caused by the transmission. This means that the ideal channel can provide the receiver with a distortionless signal that is as close to the output of the transmitter as possible and differs from it only by a constant gain factor and a constant delay. Using the third canonical signal of Eq. 5.6, the received distortionless signal becomes
| \[ r(t) = \Re\left\{ Kg(t-\tau_g) e^{i\left[\omega_c t + \varphi(\omega_c)\right]} + n(t) \right\} \] | (5.8) |
where the complex envelope is attenuated by a constant factor \(K\), delayed by group delay \(\tau_g\), and suffers a carrier-dependent phase shift \(\varphi(\omega_c)\). Ideally, these changes are negligible and/or are compensated for by the receiver.
A central design consideration in communication engineering is choosing the type of signaling, which entails a specific kind of modulation at the transmitter and a corresponding demodulation at the receiver. The particular choice may have different advantages in terms of the attainable signal-to-noise ratio for a given bandwidth (which is proportional to the maximum information rate in the channel), robustness to noise and distortion, and ease and cost of technical implementation. In turn, these considerations may be constrained by the available channels in the electromagnetic spectrum (at least in wireless communication). The choice of channel depends on the power that is required and available for transmission, the absorption characteristics of the medium in the particular frequency range, dispersion profile with respect to bandwidth, the distance that the signal should travel, interference from other communication in overlapping channels, susceptibility to eavesdropping and jamming, effects of finite wavelength on transmission, and more.
At the receiver, two different kinds of detection methods are distinguished. Noncoherent detection uses the signal alone for demodulation with no additional inputs. Commonly, it allows for neglecting the carrier phase, which makes it attractive for AM reception. However, it is possible to demodulate FM and PM noncoherently as well. Coherent detection involves an additional input from a local oscillator that is used to eliminate the carrier through destructive interference, and therefore retain the phase information. Coherent detection is generally (but not universally) able to achieve better signal-to-noise ratio, remove phase distortion, and follow potential carrier frequency drift. However, it tends to be more complicated and costly to implement. Some modulation types, like QM, for example, can only be demodulated using coherent detection. Others, like FM, can be demodulated in both ways, but tend to benefit significantly from coherent detection.
A generalized receiver that can demodulate an arbitrary signal is shown in Figure 5.2 (bottom diagram). The receiver has a local oscillator that can constitute the coherent source, if necessary. In some receivers, before fully modulating the signal to obtain the baseband, a modulated intermediate frequency is obtained, which can be advantageous for removing interference and for filtering in the carrier band. This stage is also optional.
In modern communication technology that transmits digitally coded information, coherent detection has another critical feature—it enables the receiver to fully synchronize with the transmitter. This can have different advantages, depending on the application. For example, the clock of a synchronized receiver can be synchronized to the transmitter, so that signal processing can be made much more precise and flexible, without additional layers of sampling and resampling that can exacerbate potential phase distortion and errors.
Advanced communication techniques sometimes incorporate multiple carriers or a wideband spectrum as carrier. By increasing the bandwidth, they can have advantages in achieving better signal-to-noise ratio and lower error rate, or even reduce the likelihood of eavesdropping or interference. Such techniques may be more complex and expensive to implement. However, the same general building blocks and principles guide the design of wideband systems as narrowband and single-carrier communication.
5.3.2 Acoustic and auditory communication
The analysis of the auditory system and its acoustic environment poses an inverse problem to what is paradigmatically solved in communication engineering. Instead of designing a signaling system based on general requirements, we would like to see how communication can arise from naturally occurring acoustic signals and from the auditory system existing design. As is discussed in §3.5, the majority of acoustic signals can be represented most generally in the form of a sum of AM-FM narrowband modes (Eq. §3.25). This representation can be justified based on the physical acoustics of typical sources, on the realistic necessity to represent their transient properties, and on the effects of the environment. Thus, the typical broadband acoustic signal is a superposition of narrowband signals that are suitable for communication, as in Eq. 5.6. This matches with the canonical transmitter design in communication, only with the option for multiple carriers. Therefore, many acoustic sources are natural candidates for being a communication transmitter of acoustic signals. Acoustic sources that are stochastic and do not have a fixed carrier can still be modulated and are amenable to noncoherent reception methods.
Acoustic signals that propagate in the environment are susceptible to various distortions such as dispersion, reflections, and effects of variable weather conditions, as was discussed in §3.4. As a rule, the first wavefront to arrive to the ear is the least distorted one and has the highest likelihood to retain a form—and in particular a phase function—that is closest to the original source. Additionally, the acoustic receiver picks up noise from the environment and interference from competing sources that occupy the audio range, which is also considered to be noise.
It is worth dwelling on the concept of noise, which has several related meanings that have been used somewhat interchangeably in traditional hearing research. One meaning is “unwanted sound” (e.g., Schafer, 1994, p. 273), which in research can be any out-of-context sound source, according to how it is defined by the experimenter who has also designed the hearing task. In signal processing and much of classical psychoacoustics, noise has been modeled as white noise, or a spectrally weighted version of it. In communication theory, white Gaussian noise is appropriate, because it exactly models (random) thermal noise, which is indeed the most conspicuous noise type in electronic circuitry. However, other types of unwanted signals according to the communication jargon would be considered interference, but not noise. The acoustic equivalent would be competing speech and other non-random sources from the environment. As will be seen in §9.9.2, there is an aspect of noise that is relative and is determined by the ability of a system to track the incoming signal. When the signal is too fast and too unpredictable to track, it can be considered noise. Therefore, constraining the range in which the “noise-signal” can vary, e.g., by a filter, removes some of the unpredictability and makes it somewhat less noise-like, as would be in the unfiltered version. Because the audio range has such low frequencies involved compared to electromagnetic communication, this has some implications on low-frequency auditory processing.
These acoustic communication challenges are qualitatively identical to those experienced in communication across electromagnetic channels. Whether the transmission is in radio, microwave, or light frequencies, it is susceptible to atmospheric dispersion and absorption effects, to reflections, and to variable weather conditions49. Multipath propagation is the analogous concept in communication engineering to reverberation in acoustics, but is more general. Its effects may be detrimental to reception (e.g., Saleh and Valenzuela, 1987). Both phenomena are characterized by pulse broadening.
As a receiver, the auditory system has mechanisms that are suitable for both coherent and noncoherent detection. In demodulating AM, noncoherent detection is the most straightforward detection as it requires envelope extraction and it discards the carrier phase through squaring. One of the simplest envelope detector designs is a half-wave rectifier, which coincides with the mechanoelectric transduction input-output response, as no spiking occurs during the hyperpolarizing phase of the inner hair cell receptor potential (Brugge et al., 1969; Russell and Sellick, 1978; Joris and Yin, 1992). Depending on the particular low-pass filtering that exists in the transduction stage, some of the phase information is retained after rectification (Heil et al., 2013; Sanderson et al., 2003). At the same time, the auditory system exhibits neural phase locking (estimated to be effective below about 4 kHz in humans), which means that the phase of the incoming signals can be conserved in transduction from mechanical signals. This is a necessary condition for coherent detection, which is ideally suited for FM, but can also improve the performance of most other demodulation types. See §6.4 for a further review of the auditory sensitivity to both AM and FM.
All in all, the auditory system has the same features as a generic communication system, as long as the acoustic object is treated as a transmitter. Then, the mathematical form of the signal, the effect of the channel, and the basic operations performed at the auditory receiver, are all standard parts of the communication signal processing. The only missing component is the messaging intent from the side of the transmitter, which is anyway not modeled mathematically. In communication, it is assumed that there is an agent behind the transmitter that tries to send an informative message to the receiver. Behind the receiver there is also an agent who accepts the recovered message. Modulation of acoustic sounds, however, is not always intentional and can be caused by the oscillator itself (e.g., by beating modes or nonlinear transients), or by transformations imposed in propagation through the medium (§3.3.3). This means that not all modulation in sound necessarily stand for intentionally sent information. Putting it all together, we can reframe the acoustic-auditory signal processing chain as a potential communication system, which can become de-facto communication if the roles of information source and destination are engaged. Given that the potential and the de-facto communications are mathematically indistinguishable, they are both amenable to the same analytical concepts and tools of communication theory. Conceptually, this logic transforms the acoustic wave to an acoustic signal.
That hearing can be formally recast as a communication system is hardly a surprising conclusion, since its role in communication is ingrained in much of human and other animal life. Thus, robust “coupling” between active cortical brain areas of talker and listener is to be expected and has indeed been demonstrated, representing the message origin and destination (Stephens et al., 2010). Still, while the communication engineering jargon and background has been in some use in auditory research, the analogy has not been pursued to a great length (e.g., Truax, 2001; p. 11; Brumm and Slabbekoorn, 2005, Blauert, 2005) and it has never been formally integrated into the auditory theory.
The novelty of the present approach, then, is that the link between communication and hearing is made openly and is based on more intricate mathematical and functional similarities. Borrowing from communication here is not done in a metaphorical way, but rather as a well-justified analytical step. Nevertheless, we shall use a rather limited set of qualitative results from communication, namely, the classification to detection types, and the theory of phase-locked loops for coherent detection (§9). While this leaves much room for borrowing more ideas from communication, it will be sufficient in combination with our main concern of the imaging nature of the system. With this in mind, let us turn to optical imaging as see how it relates to communication.
5.4 Imaging and communication
The basic principles of imaging systems were presented briefly in §4. Imaging and communication are in many respects complementary (Rhodes, 1953), but present different ways of thinking, which occasionally overlap in optical communication applications. However, there are several parallels and differences between the imaging and communication perspectives, which limit the extent of the analogy and have to be clarified first. In this section we will show how an imaging system can be interpreted as a communication system and highlight some of the similarities and differences between the two disciplines.
It is going to take much more work to prove that the auditory system can be rigorously interpreted as an imaging system than it has taken us to prove that it is a communication system, so it will be deferred to §§ 10 to 12.
5.4.1 Imaging as communication
A block diagram of the most basic single-lens imaging system is given in the bottom of Figure 5.1. Unlike the general communication system, message transmission is optional. Furthermore, the modulation is two-dimensional spatial rather than one-dimensional temporal. Instead of a transmitter, we have an object that modulates a light source carrier. Thus, the order of the carrier and modulation operations is inverted compared to a standard transmitter, but the resultant signal is mathematically identical and can take the canonical communication signal form of Eq. 5.6, as long as the modulation and carrier domains are separated. However, a random carrier is a better model for sunlight and most artificial light sources than a sinusoidal (monochromatic) carrier, as was considered in §5.3.1.
The light propagation in the medium is a form of diffraction—a quadratic phase transformation that varies along the cross-section of the wavefront, normal to the optical axis (see §4.2.2). Over long distances, absorption, dispersion, and atmospheric disturbance may have a significant effect on the image quality and visibility, just like in other radiation types. Noise is something that is less of an issue in normal daylight conditions, but can become significant in low-light imaging. For example, stargazing is highly sensitive to light pollution, and it is impossible in daylight with the naked eye and difficult even with a telescope.
The light signal enters the lens and its extent is limited by the aperture (which is sometimes the lens itself). The lens is optional when the aperture is very small (a pinhole camera imaging system). The light propagates further to the screen, where an image is formed that can be demodulated by a suitable detector and further processed from there. The detection that is applied in vision is noncoherent—the carrier phase plays no role in the image formation on the retina, which results in incoherent intensity imaging.
If we recast the lens, aperture, and internal diffraction as a signal-processing stage, then the analogy to the generic communication receiver becomes clearer. Hence, the transmitter is a combination of the object information source, while the light source generates the carrier. Then, the optical medium is the channel, and the receiver comprises the imaging system elements—the lens, aperture, second diffraction, screen, and detector.
While imaging is clearly similar to a generic communication system, there is no mandatory messaging intent that is associated with the transmission, just as was the case in the auditory-communication analysis above. But functionally there is no difference, as the modulation and subsequent transmission and demodulation take place anyway. Nevertheless, sending information is once again true in potential using the imaging system, which is mathematically set up as a spatial communication system. It conceptually transforms the optical wave into a signal.
5.4.2 Similarities and differences between imaging and communication
Despite the clear high-level similarities between imaging and communication, it is worth drawing a more nuanced comparison that can sharpen the uniqueness and strength of each approach.
The standard goal of imaging is expressed as an ideal image—a geometrical replica of the original spatial pattern that only differs by a constant factor (Eq. §4.1). This is somewhat analogous to the ideal transmission through a distortionless channel, which only differs by a constant gain factor and a constant delay (Eq. 5.8). The temporal delay of communication is factored in the different coordinate systems of the spatial object and image, which are separated by their distance. Imaging allows for magnification on the temporal domain, whereas gain is scaling of level only, so for the two ideals to be the same, the magnification must be set to unity.
The most obvious difference between imaging and communication is the number of dimensions that are actively involved. Imaging is spatial and is usually taken as two-dimensional, but can be also one- or three-dimensional, or even four-dimensional when motion is considered. The signal processing of the image is spatial and not temporal, so it is a function of the position. The temporal factor is implicit in the high-frequency carrier (often omitted due to harmonic time dependence). However, it may be explicitly included in the imaging by temporally modulating the object features, or through relative motion of the object and the imaging system. Communication is primarily temporal and its spatial extent is irrelevant for most signal processing. Spatial considerations in communication enter the design only in the antenna, or when the channel or electronic components have to be modeled as transmission lines, for relatively short carrier wavelengths compared to the dimensions of the electronics.
The basic components in the signal processing of the image are based on all-pass quadratic phase transformations, which do not have counterparts in communication. Additionally, single-lens imaging is modeled as a double Fourier transform in the modulation domain as a result of the lens curvature and the diffraction. But this highlights a deeper difference in the approaches of the two perspectives. The signal processing of imaging, including the Fourier transforms, is calculated in the modulation domain, which is taken as independent from the carrier. In communication, it is done primarily in the carrier domain, even if the ultimate concern is the baseband (demodulated) domain. However, convenient transformations exist between bandpass to low-pass filter transfer functions, which essentially relate to the modulation domain as well and can be used to draw additional parallels (Couch II, 2013; pp. 248–250).
In communication, the type of modulation has to be designed or programmed in the transmitter and receiver. In standard imaging theory as applied in vision, complex modulation fully describes the object and is demodulated as (spatial) AM, although spatial FM effects can be visually observed as well (Stromeyer III and Klein, 1975). Therefore, an intensity image is obtained based on the spatial modulation pattern. With coherent imaging that is limited to a monochromatic light source, it is possible to conserve the phase and obtain an amplitude image. However, such an image would typically appear only as an intermediate stage, as the eye and standard optical equipment cannot detect the fast amplitude variations and require conversion to intensity images as the final format.
Communication emphasizes the minimization of errors in the recovered message that are caused by distortion and noise. Imaging attempts to minimize aberrations of any kind, which are well-defined forms of distortion in one, two, or three dimensions. Aberrations are not usually presented as imaging errors per se, but optical designs usually try to correct them just as well (Mahajan, 2011). Aberrations are determined by the imaging system and the object properties, which make them deterministic. Communication errors are random, whereas distortion may be random if it arises in the channel, or deterministic if it arises in the receiver signal processing. In the latter case, carefully designed systems try to minimize these distortions.
In addition to aberrations, imaging has several conceptual tools that are intuitive and do not have clear analogs in communication. First and foremost, the image can be focused or blurry. The focused image relates to the condition in which the different quadratic phase transformations exactly cancel out. It is somewhat analogous to the receiver signal processing that should precisely invert the signal processing done by the transmitter. However, a markedly blurry communication would be deemed distorted and possibly ridden with errors, with no special value for the receiving agent. In contrast, in vision, the blurry image provides information about the relationship between foreground and background, and sometimes about the distance from the object, the available light, the object colors, or the state of the optical system (in cameras). Therefore, there are more degrees of freedom in image interpretation than there are in standard communication, which is tailored to more specific requirements.
Finally, unless it is also temporally modulated, the spatial image exists “in parallel”, or simultaneously, whereas the received communication is obtained sequentially. Image processing, however, can still be sequential (e.g., by scanning the image), although the spatial order of processing needs not be linear.
Footnotes
45. The requirements for a unique entropy function are: 1. The measure should be continuous with respect to probability. 2. When all symbols appear with equal probability, the amount of information carried by each symbol is inversely proportional to the number of symbols in the set. 3. The total information expressed by a certain choice (represented by a symbol) should remain invariant to branching to several sub-choices—each of which contains a smaller amount of information. In other words, if the symbol is replaced with a number of symbols, they would together carry the same amount of information as that one symbol. 4. The measure should be normalized to yield 1 bit of information when there are two symbols with equal probabilities. Implicit to these requirements is that probability theory—itself can be derived from three postulates—is valid. It is, however, possible to invert the logic and assume that information is the more primitive concept and derive probability theory from it instead (Ingarden and Urbanik, 1962). This unusual approach is important to attest to the primacy of the information as was defined by Shannon.
46. Strictly speaking, the channel is taken to be “memoryless”, which means that the present output is determined by the present input, independently of past inputs. The various bounds on channel capacity are unaffected by the presence of feedback in the channel (but see Massey, 1990).
47. The sampling theorem has been discovered several times before it was popularized by Shannon (Luke, 1999).
48. While uncommon over large distances, it is also possible to communicate the message directly in baseband, without a carrier.
49. The electromagnetic signal may be also susceptible to effects that are strictly electromagnetic arising from conducting surfaces, charged objects, magnetization, polarization, etc.
References
Attneave, Fred. Some informational aspects of visual perception. Psychological Review, 61 (3): 183, 1954.
Barlow, Horace B. Possible principles underlying the transformations of sensory messages. In Rosenblith, Walter A., editor, Sensory Communication. Contributions to the symposium on principles of sensory communication, July 19–August 1, 1959, Endicott House, M.I.T., pages 217–234. M.I.T. Press, 1961.
Ben-Naim, Arieh. A Farewell to Entropy: Statistical Thermodynamics Based on Information. World Scientific Publishing Co. Pte. Ltd., Singapore, 2008.
Blauert, Jens. Analysis and synthesis of auditory scenes. In Blauert, Jens, editor, Communication Acoustics, pages 1–25. Springer-Verlag Berlin Heidelberg, 2005.
Brette, Romain. Is coding a relevant metaphor for the brain? Behavioral and Brain Sciences, 42: 1–58, 2019.
Broadbent, Donald Eric. Perception and communication. Pergamon Press Ltd., Oxford, England, 2nd reprint edition, 1958/1966.
Brugge, John F, Anderson, David J, Hind, Joseph E, and Rose, Jerzy E. Time structure of discharges in single auditory nerve fibers of the squirrel monkey in response to complex periodic sounds. Journal of Neurophysiology, 32 (3): 386–401, 1969.
Brumm, Henrik and Slabbekoorn, Hans. Acoustic communication in noise. Advances in the Study of Behavior, 35: 151–209, 2005.
Chechik, Gal, Anderson, Michael J, Bar-Yosef, Omer, Young, Eric D, Tishby, Naftali, and Nelken, Israel. Reduction of information redundancy in the ascending auditory pathway. Neuron, 51 (3): 359–368, 2006.
Cherry, E Colin. Some experiments on the recognition of speech, with one and with two ears. The Journal of the acoustical society of America, 25 (5): 975–979, 1953.
Chomsky, Noam. Three models for the description of language. IRE Transactions on Information Theory, 2 (3): 113–124, 1956.
Couch II, Leon W. Digital and Analog Communication Systems. Pearson Education Inc., Upper Saddle River, NJ, 8th edition, 2013.
Cover, Thomas M and Thomas, Joy A. Elements of information theory. John Wiley & Sons, Hoboken, NJ, 2006.
Garson, Justin. The birth of information in the brain: Edgar Adrian and the vacuum tube. Science in Context, 28 (1): 31–52, 2015.
Gwilliams, Laura and Davis, Matthew. Extracting language content from speech sounds: An information theoretic approach. In Holt, Lori, Peelle, Jonathan E., Coffin, Allison B., Popper, Arthur N., and Fay, Richard R., editors, Speech Perception, volume 74, pages 141–172. Springer Nature Switzerland AG, Cham, Switzerland, 2022.
Heil, Peter, Verhey, Jesko L, and Zoefel, Benedikt. Modelling detection thresholds for sounds repeated at different delays. Hearing Research, 296: 83–95, 2013.
Ingarden, Roman and Urbanik, Kazimierz. Information without probability. IX (1): 131–150, 1962.
Jacobson, Homer. The informational capacity of the human ear. Science, 112 (2901): 143–144, 1950.
Jacobson, Homer. Information and the human ear. The Journal of the Acoustical Society of America, 23 (4): 463–471, 1951b.
James, William. The Principles of Psychology in Two Volumes. Vol. I. Henry Holt and Company, New York, 1890. 1931 print.
Joris, Philip X and Yin, Tom CT. Responses to amplitude-modulated tones in the auditory nerve of the cat. The Journal of the Acoustical Society of America, 91 (1): 215–232, 1992.
Jumarie, Guy. Maximum Entropy, Information without Probability and Complex Fractals: Classical and Quantum Approach. Springer Science+Business Media Dordrecht, 2000.
Kahneman, Daniel. Attention and Effort. Prentice-Hall, Inc., Englewood Cliffs, NJ, 1973.
Landauer, Rolf. Irreversibility and heat generation in the computing process. IBM Journal of Research and Development, 5 (3): 183–191, 1961.
Landauer, Rolf. The physical nature of information. Physics Letters A, 217 (4-5): 188–193, 1996.
Ling, Fuyun. Synchronization in Digital Communication Systems. Cambridge University Press, Cambridge, England, 2017.
Luce, R Duncan. Whatever happened to information theory in psychology? Review of General Psychology, 7 (2): 183–188, 2003.
Luke, Hans Dieter. The origins of the sampling theorem. IEEE Communications Magazine, 37 (4): 106–108, 1999.
Mahajan, Virendra N. Aberration Theory Made Simple, volume TT93. SPIE Press, Bellingham, WA, 2nd edition, 2011.
Massey, James. Causality, feedback and directed information. In Proc. Int. Symp. Inf. Theory Applic.(ISITA-90), pages 303–305. Citeseer, 1990.
Middleton, David. An Introduction to Statistical Communication Theory. IEEE Press, Piscataway, NJ, 1996. 2nd reprint edition; originally published in 1960.
Miller, George A and Licklider, Joseph CR. The intelligibility of interrupted speech. The Journal of the Acoustical Society of America, 22 (2): 167–173, 1950.
Miller, George A and Nicely, Patricia E. An analysis of perceptual confusions among some English consonants. The Journal of the Acoustical Society of America, 27 (2): 338–352, 1955.
Miller, George A. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63 (2): 81, 1956.
Neisser, Ulric. Cognitive Psychology. Psychology Press, Hove, England, classic edition edition, 2014. First published in 1967.
Nelken, Israel and Chechik, Gal. Information theory in auditory research. Hearing Research, 229 (1-2): 94–105, 2007.
Nizami, Lance. Information theory is abused in neuroscience. Cybernetics & Human Knowing, 26 (4): 47–97, 2019.
Nyquist, Harry. Certain topics in telegraph transmission theory. Transactions of the American Institute of Electrical Engineers, 47 (2): 617–644, 1928.
Perkel, Donald H and Bullock, Theodore H. Neural coding. Neurosciences Research Program Bulletin, 6 (3): 221–348, 1968.
Pierce, John R. An Introduction to Information Theory: Symbols, Signals and Noise. Dover Publications, Inc., Mineola, NY, 2nd edition, 1980.
Proakis, John G. and Salehi, Masoud. Fundamentals of Communication Systems. Pearson Education, Inc., Upper Saddle River, NJ, 2nd edition, 2014.
Rhodes, J Elmer. Microscope imagery as carrier communication. Journal of the Optical Society of America, 43 (10): 848–852, 1953.
Rieke, Fred, Warland, David, van Sleveniunck, Rob de Ruyter, and Bialck, William. Spikes: Exploring the Neural Code. MIT Press, Camridge, MA and London, England, 1999.
Russell, IJ and Sellick, PM. Intracellular studies of hair cells in the mammalian cochlea. The Journal of Physiology, 284 (1): 261–290, 1978.
Saleh, Adel AM and Valenzuela, Reinaldo. A statistical model for indoor multipath propagation. IEEE Journal on Selected Areas in Communications, 5 (2): 128–137, 1987.
Sanderson, Mark I, Neretti, Nicola, Intrator, Nathan, and Simmons, James A. Evaluation of an auditory model for echo delay accuracy in wideband biosonar. The Journal of the Acoustical Society of America, 114 (3): 1648–1659, 2003.
Schafer, R Murray. The Soundscape: Our Sonic Environment and the Tuning of the World. Destiny Books, Rochester, VT, 1994.
Sendra, Sandra, Lloret, Jaime, Jimenez, Jose Miguel, and Parra, Lorena. Underwater acoustic modems. IEEE Sensors Journal, 16 (11): 4063–4071, 2015.
Shannon, Claude E. A mathematical theory of communication. The Bell System Technical Journal, 27 (3): 379–423, 623–656, 1948.
Shannon, Claude E. The bandwagon. IRE Transactions on Information Theory, 2 (1): 3, 1956.
Shannon, Claude E and Weaver, Warren. The mathematical theory of communication (Urbana, IL. University of illinois Press IL, 1949.
Stephens, Greg J, Silbert, Lauren J, and Hasson, Uri. Speaker–listener neural coupling underlies successful communication. Proceedings of the National Academy of Sciences, 107 (32): 14425–14430, 2010.
Stojanovic, Milica, Catipovic, Josko, and Proakis, John G. Adaptive multichannel combining and equalization for underwater acoustic communications. The Journal of the Acoustical Society of America, 94 (3): 1621–1631, 1993.
Stromeyer III, CF and Klein, S. Evidence against narrow-band spatial frequency channels in human vision: The detectability of frequency modulated gratings. Vision Research, 15 (8-9): 899–910, 1975.
Sumby, William H and Pollack, Irwin. Visual contribution to speech intelligibility in noise. The Journal of the Acoustical Society of America, 26 (2): 212–215, 1954.
Szilard, Leo. Über die entropieverminderung in einem thermodynamischen system bei eingriffen intelligenter wesen. Zeitschrift für Physik, 53 (11-12): 840–856, 1929. Translated by Anatol Rapoport (1964), “On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings”.
Truax, Barry. Acoustic Communication. Ablex Publishing, Westport, CT; London, 2nd edition, 2001.
Weisser, Adam. Auditory information loss in real-world listening environments. arXiv preprint arXiv:1902.07509, 2019.
Weisser, Adam. Complex Acoustic Environments: Concepts, Methods, and Auditory Perception. PhD thesis, Macquarie University, 2018.
Wheeler, John A. Information, physics, quantum: The search for links. In Zurek, Wojciech H., editor, Complexity, Entropy, and the Physics of Information. Addison-Wesley, Reading, MA, 1990.
 )
)