Chapter 7

Toward a unified view of coherence

”It seems however that the best way to reach a conclusion in the near or far future is to try and apply to optics the central problem of communication theory. In order to do this one should not indulge too much in dealing with coherent or semi-coherent illumination, frequency analysis and all straightforward translations of well-known radio communication results into optical terminology. Such topics have been perhaps a little overstressed in optics. The eye is not the ear and any interpretation of vision in terms of frequencies is really too far-fetched.” (Giuliano Toraldo di Francia, 1955)

7.1 Introduction

Hearing science is manifestly interdisciplinary and as such it has absorbed ideas and methods from numerous fields in science and engineering. As every hearing researcher brings their own expertise and perspective into the science, the collective knowledge about hearing has a distinct richness to it. This has meant that the different inputs from all these fields have often been introduced independently of one another, so they do not always readily coalesce into a coherent whole. A key example is the concept of coherence in hearing (no pun intended), which has been imported to auditory science from several different disciplines—optics, communication, and neuroscience are the primary ones—each at a different period, and often without consideration of one another. Therefore, coherence has become an ambiguous term that is not well-defined within hearing, despite its widespread use.

On an intuitive level, coherence quantifies how closely related two (or more) signals are. This can be applied to observations of the same signal at different coordinates, which correspond to different signal evolution or processing. It can also apply to different signals that originate from the same source, or to different signals that are subjected to common modulation. Essentially, coherence provides information about the identity of different signals or measurements—an identity that may be difficult to ascertain using other measures. Coherence theory has been developed mainly with respect to optics and is critical in imaging theory, as imaging is usually classified as either coherent or incoherent. It has also been used in a more ad-hoc way in communication engineering with the design of receivers that employ either coherent or noncoherent detection, which depend on whether they contain a local oscillator that can be made to track the carrier phase. In acoustics and hearing, coherence theory has been adopted in a rather sporadic manner in physical and room acoustics, signal processing, and hearing.

Synchronization is the effect of binding together the outputs of independent oscillating systems, in a way that confers the temporal pattern of one oscillator to the other. Synchronization effects have been used extensively in engineering, including in coherent detection in communication systems. Just like coherence, synchronization has also become more prominent in neuroscience as a likely universal feature of the brain operation. In parallel, synchronization effects have been identified throughout the auditory pathways as a hallmark of hearing and are gradually being recognized for their significance. From the definition of coherence above, we can see that when an output is synchronized to the input, then the two are effectively coherent. Indeed, when referring to neural transmission it is nearly synonymous to talk about it as being coherent or synchronized.

In order to track the coherence properties of the acoustic source all the way to the brain, it is necessary to have a unified view of what it is exactly that is being tracked. However, none of the available coherence theories can continuously map the entire auditory processing chain. Classical coherence theory in optics, for example, deals mostly with stochastic and stationary processes that do not represent very well the dynamic nature of the kind of signals that are regularly encountered in acoustics and hearing. Acoustic theory has a few tools that are useful in room acoustics and reverberation, but not elsewhere. Communication engineering methods may provide an adequate classification for the detection and signal processing that is desirable, at least at the interface of the auditory system with its environment, but requires committing to a specific modulation and detection method. Finally, synchronized brain activity models (auditory and others) have been completely divorced from these disciplines and they tend to remain confined to the neural domain, which makes their connection with realistic acoustic environments weak.

Optics	Acoustics
Temporal coherence	Temporal correlation
Spatial coherence	Spatial correlation
Cross-spectral density / Mutual spectral density	Coherence
Coherence length	Correlation length
Coherence time	Correlation time

Table 7.1: A jargon “thesaurus” for coherence functions used in optics and their most common counterparts in acoustics, where the optical terms were not employed. The terms from optics are adopted in this work and are explained in §8. For a few additional terms in optics see Goodman (2015, Table 5.1, p. 185).

The following contains short quasi-historical and conceptual reviews of coherence in the different domains that are relevant to hearing, which have also guided this work, to a large degree. The reviews enable the synthesis of the various perspectives, which can then form a basis for a unified understanding of the topic in general. In §8 and §9 we will provide more detailed accounts of coherence theory and synchronization, with the phase-locked loop as a primary component that is at the heart of the mammalian auditory system.

7.2 Perspectives on coherence

Because the concept of coherence has been used in somewhat different contexts within communication, optics, physical acoustics, hearing, and neuroscience, it is instructive to trace back a few of the milestones in its development in these disciplines. The short introductions below are not intended to be thorough reviews, but rather provide vignettes on different needs and systems that motivated the development of this important concept. It will turn out that hearing theory requires a hybrid approach, with elements borrowed from all the particular coherence theories. The development of optical coherence theory is reviewed in Born et al. (2003, pp. 554–557), but no such historical accounts were found for any of the other fields.

The first technical use of the term coherence appeared in one of the earliest inventions of the radio days—the coherer. It was invented by Edouard Branly in 1890, and was perfected by Oliver Lodge who patented it in 1898 (Dilhac, 2009). Lodge called it “Branly's coherer” (from Latin: cohaere—to stick). The coherer was capable of remotely detecting a spark discharge by a change in resistance of a tube filled with granules of oxide metal, as a result of an electric charge, which made metal surfaces in the vicinity of the charge momentarily “fuse together” (Garratt, 2006; p. 64). This device was widely used by Guglielmo Marconi in his early attempts for radio transmission, until more suitable inventions became available that enabled continuous wave transmission and reception at practical power levels.

7.2.1 Optics

Interference of waves was widely known since Thomas Young's famous slit experiments, and the observation of a limited region of coherence with polarized light modes has been recognized already by Verdet (1865). But coherence as a dedicated term describing waves that possess the ability to interfere may have appeared much later (Schuster, 1909; p. 60): “Two centres of radiation emitting vibrations which are related in phase owing to their having originated at the same ultimate source are said to be “coherent”.” Schuster also defined the contrary, which he did not name, but was later referred to as incoherent: “Independent sources of light even when emitting quasi-homogeneous light do not give rise to interference effects.” The coherence between two point sources that belong to an extended light source at a distance was explored by Pieter Hendrik van Cittert using statistical correlation and ideal imaging conditions, which yielded a theorem that has been used extensively in astronomy (van Cittert, 1934; van Cittert, 1939). The most formal introduction of coherence into optics was done by Frits Zernike (1938), who tied it to a quantity introduced by Albert Michelson (1890) earlier to analyze interference patterns, using the intensities of two beams of light—visibility⁶⁵

\[ V = \frac{I_{max}-I_{min}}{I_{max}+I_{min}} \]

(7.1)

where \(I_{max}\) and \(I_{min}\) refer to the maximum and minimum intensity of the fringes in the interference pattern measurement (see example in Figures 7.1 and 7.2). Zernike referred to visibility as the degree of coherence, or partial coherence, which is the important state between complete coherence and complete incoherence. He then generalized the theory and defined the complex degree of coherence and mutual intensity, and showed how they propagate to point images from a common distant source, validating earlier results by van Cittert. The theory was further simplified and was formulated using more deterministic (less statistical) principles by Pierre-Michel Duffieux (1946 / 1983) and independently by Harold Hopkins (1951), who introduced very useful connections between the degree of coherence and image formation theory. Importantly, they showed how an amplitude image is obtained with fully coherent objects, whereas in incoherent imaging, it is an intensity image that is independent of the phase. Finally, over several publications, Emil Wolf further generalized these tools to polychromatic waves and introduced more rigor to the theory, as in proving that coherence propagates according to the wave equation, amongst other contributions (Wolf, 1954; Wolf, 1955). An alternative version of the theory based on the cross-spectral density instead of the cross-correlation function was also developed by Wolf (1982), Wolf (1986) and provided tools to express partially coherent fields as incoherent sums of coherent modes.

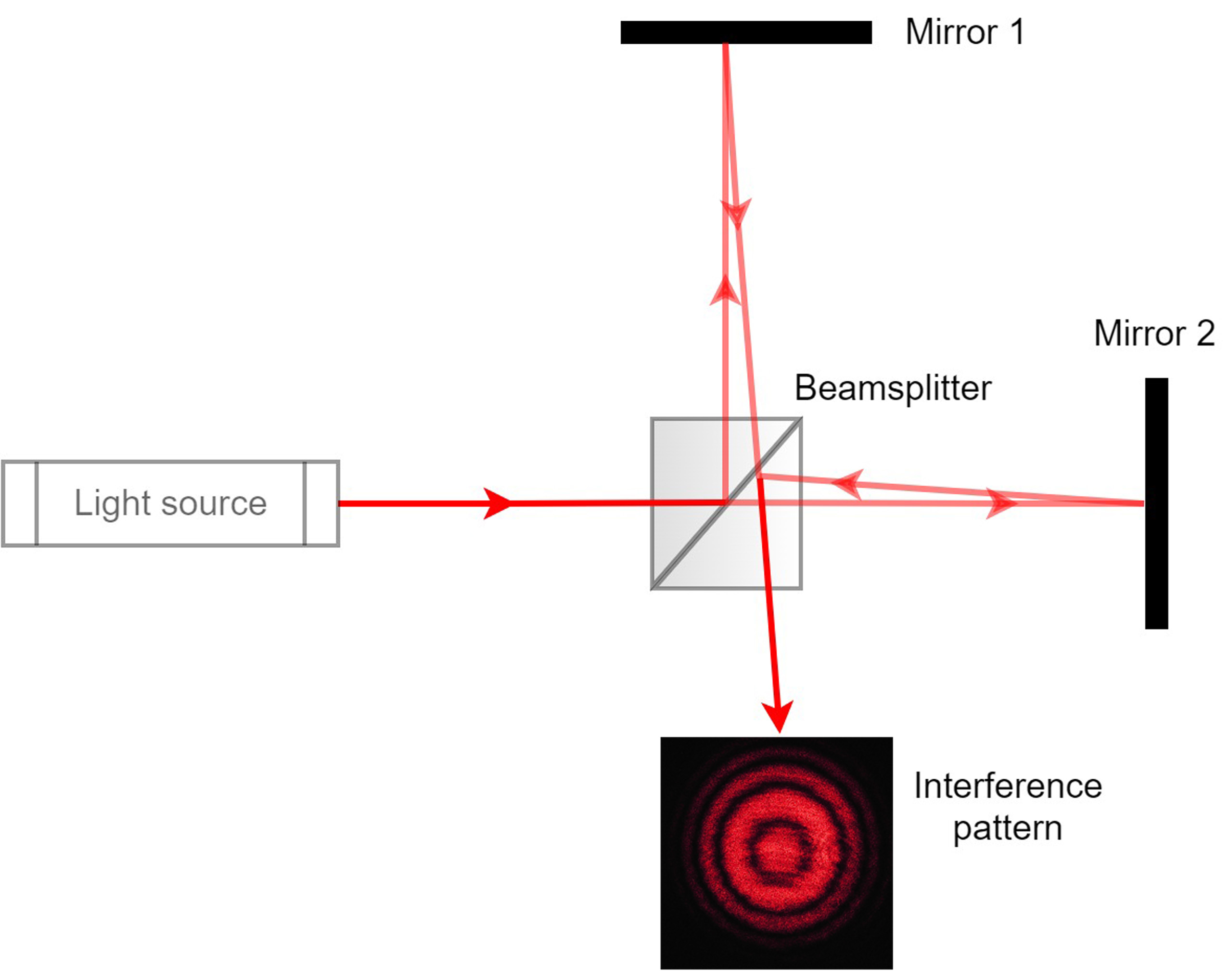
Figure 7.1: Michelson interferometer. A beam of light from a coherent source is split evenly in the beamsplitter, with one beam going toward mirror 1 and the other continuing to mirror 2. The returning beams are united at the beamsplitter and are measured at the detector, where they form an interference pattern. The interference pattern photo at the detector was obtained from a He-Ne Laser (633 nm), by FL0, https://en.wikipedia.org/wiki/File:Interferenz-michelson.jpg.

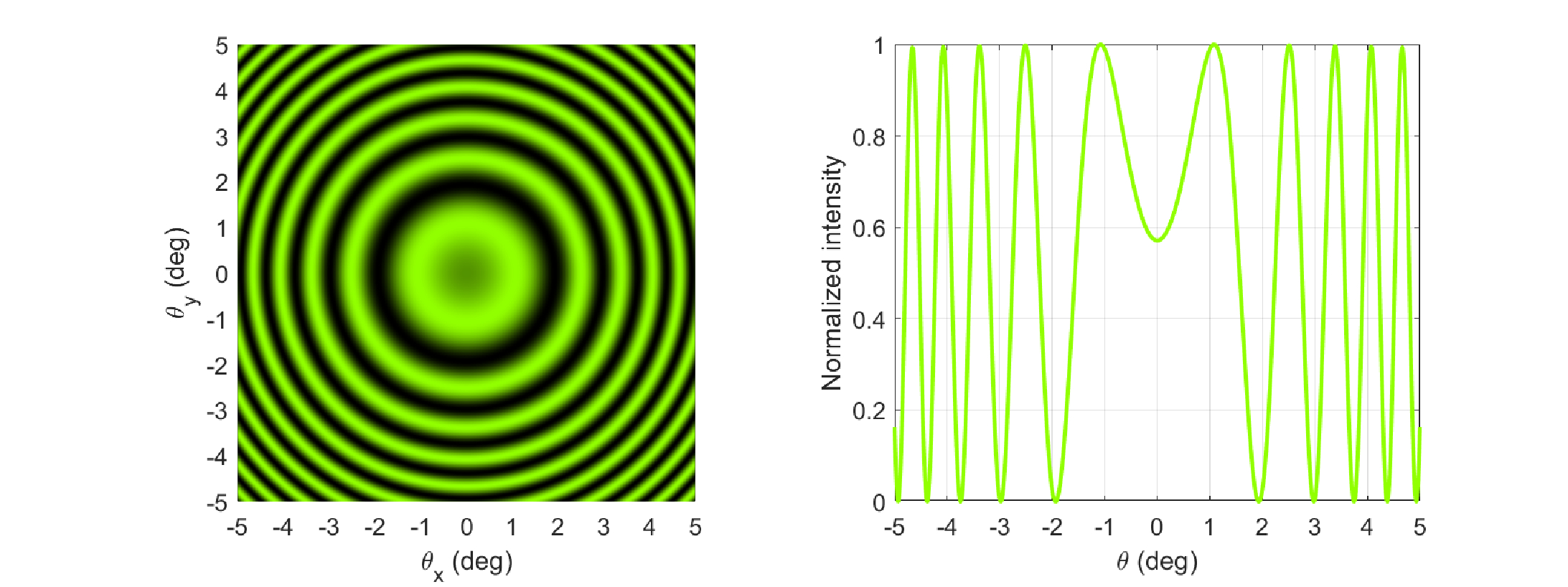
Figure 7.2: A simulated example of an interference pattern in Michelson interferometer. A monochromatic and coherent green laser beam is split in two and the beams meet at the same point on the screen (see Figure 7.1). The interference of the two fields produces the visible fringes of light intensity. The projection of the interference pattern on a flat screen is shown as a function of the angles from the optical axis (left). The one-dimensional profile of the intensity is shown on the right. The simulation was produced using a Matlab code by Ian Cooper (2019).

As the optical applications were primarily concerned with static spatial images and interference patterns, and given that light frequency is very high, coherence theory was safely formulated using stationary signals and corresponding statistical tools⁶⁶. This renders the theory ideal for time-invariant signals and systems, but is inadequate to deal with non-stationary signals and dynamic systems. A rigorous adaptation of optical coherence theory to nonstationary signals was introduced much more recently (Bertolotti et al., 1995; Sereda et al., 1998; Lajunen et al., 2005).

7.2.2 Communication

From the communication engineering side, a fundamental distinction is made between coherent and noncoherent modulation detection methods, which influences the complexity of the design and many of its characteristics (§5.3.1). The principles were discussed in some depth in Lawson and Uhlenbeck (1950), but this terminology appears to have been introduced earlier—perhaps by A. G. Emslie in 1944 (Lawson and Uhlenbeck, 1950; p. 331). This distinction exists because there are inevitable fluctuations in the carrier frequency and phase when it is generated using equipment that can drift around the channel frequency, and is transmitted over long distances in variable atmospheric conditions, and likely undergoes multipath propagation. These fluctuations amount to noise on the receiver's end, whose impact should be minimized, ideally.

In noncoherent detection, the modulation band is recovered without using the carrier phase, which is assumed to be random and uniformly distributed between \(0\) and \(2\pi\) (Viterbi and Omura, 1979; pp. 103–107, Couch II, 2013; p. 277). Noncoherent detection implies that the envelope is squared to remove all phase effects, and its most basic implementation is completely passive. The simplest example is an envelope detector that tracks the real envelope of the an amplitude-modulated carrier.

In contrast, coherent detection always requires harnessing a local oscillator in the detector that ensures that the carrier phase is tracked on a cycle-by-cycle basis, so that any phase errors are minimal. Different schemes have been devised to detect the phase, depending on the modulation method used, which often implies the use of a phase-locked loop (see §9.3).

In general, not all modulation techniques are suitable for both types of detection. The choice between coherent and noncoherent detection technique is not trivial and it depends on the specifications of the system being designed, such as the type of signaling (modulation technique) applied and the target error rate of the demodulated message.

Figure 7.3: Simplified cartoon representation of key types of coherence using arbitrary source(s) \(S\) and receiver \(R\).

7.2.3 Acoustics

Despite being applicable to all wave phenomena, application of coherence theory has been somewhat sporadic in acoustics and hearing research. Moreover, the terminology used in acoustics usually draws on that used in stochastic processes instead of wave theory. This is inconsistent with the optical and communication terminology and may have created some confusion (Table 7.1).

The first usage of the term coherence for sound waves may have been in the context of room acoustics. Morse and Bolt (1944) analyzed the steady-state response of point sources in rooms and drew the distinction between coherent and incoherent waves. Coherence here relates to the direct sound from the source and (and sometimes to the first reflection), which has a deterministic direction. Incoherence is the residual sound that is reflected from the walls. It does not have a deterministic direction and has to be analyzed in terms of its power—neglecting the phase. This distinction underlies the treatment of wave acoustics (coherent) versus statistical and geometrical acoustics (incoherent), which is often not clear-cut. Typically, in the statistical approximation rooms are taken to be large, highly reflective, and irregular in shape.

Several additional studies about coherence appeared somewhat later. Cook et al. (1955) investigated the effect of a reverberation chamber acoustics on random sound fields using cross-correlation⁶⁷. The authors defined a random sound field as one that has uniform probability to propagate in any direction and with any phase around a frequency band over sufficiently long time. They derived the theoretical correlation coefficients as a function of distance for fields in two and three dimensions. These expressions were then compared to measurements of a broadband source in a reverberation chamber, which had to be averaged over a duration of 12 s in order to match the theoretical prediction. Save from the finite integration time, the correlation coefficient of Cook et al. (1955, Eq. 1) is identical to the real part of the degree of coherence in optics (e.g., Born et al., 2003, Eq. 10.3.10, and Eq. §8.9). Similarly, Schroeder (1962) obtained an expression for the autocorrelation of the frequency response functions of large rooms (with high modal density), as a function of spectral distance. Morse and Ingard (1968, pp. 329–323) introduced expressions for acoustic sources that fluctuate too randomly to be modeled using anything but their autocorrelation function. They provided an estimate for the source correlation length and correlation time—quantities that indicate how far and long the spatial and temporal correlations remain high, respectively. While these definitions convey the same information as the coherence length and time in optics (e.g., Born et al., 2003, p. 554), they have considerably fewer applications. Coherence of acoustic fields, however, finds a greater role in the analysis of propagation and scattering in random media (e.g., turbulence), where acoustic and electromagnetic waves have been often treated together (Tatarskii, 1971; Ishimaru, 1978a; Ishimaru, 1978b).

The standard definition of coherence adopted in acoustics is taken from signal processing theory. It follows Norbert Wiener's coherency matrix theory, which was defined using the linear combination of the cross term between a set of complex time signals (Wiener, 1928; Wiener, 1930; pp. 182–195). When the functions do not interfere, the coherency matrix is diagonal, which can then represent incoherent waves that do not interact. If the functions are not independent, their coherency matrix can be diagonalized. Similarly, the squared coherency function is defined in the context of spectral analysis methods in order to deal with stochastic signals and linear systems (Jenkins and Watts, 1968). The coherency function gives a dimensionless measure of the correspondence between the output and the input (between 0 and 1, for completely uncorrelated and completely correlated, respectively). Along with the phase spectrum, coherency gives a complete description of the system. Coherency, which is also referred to as the normalized cross-spectral density function, is related to the standard coherence measure in acoustics today simply by squaring (e.g., Shin and Hammond, 2008; pp. 284–287). For systems with additional inputs, partial coherence designates the contribution of each input to the total coherence function of the output (Shin and Hammond, 2008; pp. 364–370), which is unrelated to the definition of partial coherence in optics. See also Paez (2006) for a historical review of stochastic signal processing concepts. Notably, Derode and Fink (1994) suggested a correction to the standard optical definition of coherence that makes it suitable to be adopted in acoustics, by generalizing it to nonstationary signals (e.g., pulses). This correction mainly targets applications in ultrasound.

7.2.4 Hearing: Psychoacoustics

In hearing, the coherence terminology has been used in two somewhat different contexts. Initially, it was applied to binaural processing, which is thought to cross-correlate between the left- and the right-ear signals, corresponding to the interaural phase difference (Licklider, 1948). Listeners are remarkably sensitive to changes in the interaural coherence, which also affects the perceived source size (the apparent source width) (Jeffress et al., 1962).

The second context in which coherence is used in hearing emphasizes the simultaneity of sound components or events, regardless of whether they are monaural or binaural. The term “coherence” was used by Cherry and Sayers (1956) for discussing dichotic signals that were played with variable delay between the two ears. The stimulus coherence (perceptual fusion or integration) was determined according to how its perceptual location moved on the horizontal plane (instead of being perceived as separated). Temporal coherence was later defined as “the perceived relation between successive tones of a sequence, characterized by the fact that the observer has the impression that the sequence in question forms a whole which is ordered in time” (van Noorden, 1975). McAdams (1984, p .181) further defined, “It is possible to focus one's attention on a given stream and follow it through time; this means that a stream, by definition, exhibits temporal coherence.”

Unlike optics and communication, coherent events in the psychoacoustic parlance entail that different frequency components of a broadband sound have exactly the same envelope—that they are comodulated (Figure 7.3)—even if the carrier phases are unrelated (inharmonic). This definition of temporal coherence found extensive use in auditory scene analysis (Bregman, 1990) and is conceptually closer to the modern use of the term in auditory research, which is itself influenced by similar ideas in neuroscience⁶⁸.

7.2.5 Neuroscience

An influential brain function theory, the temporal correlation hypothesis, argues that synchronized activity in networks of neurons (cell assemblies) can explain how the brain recognizes and attends to visual objects, by enhancing their features using neural networks with feedback (Milner, 1974). In his independent formulation of this theory, Malsburg (1981) generalized the hypothesis to arbitrary modalities and included processes between perception and thought. According to his theory, the dynamics of the network activity is determined by the synaptic conductivity that may be modulated on very short time scales (\(<1\) s). Such dynamics may also be suitable for forming mental objects and separating them from the background. The main motivation was to explain how the brain produces specific responses to a nearly infinite set of possible objects in the external world. Initially, Malsburg used the term “correlation”, which was not well-defined, but later became more concrete with the requirement that cross-correlated cortical neural activity should be synchronized on a millisecond time scale (Singer and Gray, 1995). The temporal correlation hypothesis has been developed mainly with respect to cortical processing and to the binding problem⁶⁹ of different features within one modality that are thought to be processed in localized areas of the visual cortex. However, coherence at different frequencies over large distances between different brain areas has been demonstrated (Varela et al., 2001). These ideas were further generalized to account for binding of multisensory features (Senkowski et al., 2008). In quantifying neural synchrony between different cortical assemblies, a distinction has been made between phase-locking or temporal synchronization and amplitude correlation (Lachaux et al., 1999). According to Lachaux et al, coherence captures both phase and amplitude similarities, but temporal synchrony is a much more sensitive and critical quantity in the brain.

7.2.6 Hearing: Neurophysiology

The amalgamation of the second coherence meaning in psychoacoustics and ideas from neuroscience have heralded a refined usage of the term in auditory neurophysiology. Here, the perspective of neural temporal correlation has been applied to auditory object-formation models as well, which, incidentally, may have started with an early attempt to account for the cocktail party problem (Malsburg and Schneider, 1986). What may be unique in auditory temporal coherence, unlike spatial images in vision (and most other modalities), is the highly dynamic nature of sound streams that allows direct correlation at the scale of temporal unfolding of stimuli and their corresponding synchronized brain response. Synchronized cortical processing is thought to manifest through selective attention to specific sound events, which exhibits synchronization across different channels following tonotopy (Elhilali et al., 2009). This is expected to be representative of many spectrally-rich natural stimuli, whose spectral components are comodulated (Nelken et al., 1999) and are preferentially processed together in the auditory cortex (Barbour and Wang, 2002). This was referred to, yet again, as “temporal coherence”, which was redefined—“temporal coherence between two channels ... denotes the average similarity or coincidence of their responses measured over a given time-window” (Shamma et al., 2011). The latter definition specifically refers to cortical (i.e., slow) neural synchronicity between common features of acoustic events, which is perceived on scales of 50–500 ms (\(<\) 20 Hz) and can be made more coherent through attention. It is distinguished from incoherent responses that may be part of the same auditory stream, but are not attended to. Although the cited research mainly discussed processing in the cortex or thalamus, we will be more interested in the upstream temporal activity that precedes these high-level effects—something which has been highlighted in the context of temporal coherence in recent studies as well (Viswanathan et al., 2022). See Elhilali (2017, pp. 115–122) for a recent review of auditory temporal coherence and alternative object formation models.

7.3 Synthesis

The quote by Toraldo di Francia (1955) that was cited in the preamble provides an ironic historical vignette that is triply wrong. The author suggested to not dwell on the question of coherence and frequencies in optics as would be more relevant for communication and for the ear. Since then, Fourier optics has been vindicated and become much more mainstream, so that the question regarding the relevance of coherence to imaging is no longer in doubt⁷⁰. But the reader of this quote may also get the false impression that acoustics and hearing science had been invested in the study of coherence back in the 1950s, which was barely the case, save for a handful of studies that were cited above. Moreover, the author compared the spatial frequencies of optics to the audio frequencies of hearing, which are two separate domains that should not be compared (although they often are). However, the reviews above should enable us to pick up from the point where di Francia left us, and motivate us to strengthen some of the connections between optics, acoustics and communication.

The six perspectives on coherence that were outlined above are at least partially incongruent. The definitions in optics and acoustics are easily merged, as long as we are careful to use a common terminology. In most (but not all) texts in acoustics, acoustical correlation is the same as optical coherence, whereas acoustic coherence is the cross-spectral density in optics (see Table 7.1). Similarly, the interaural cross-correlation is functionally identical to spatial coherence in optics (§8.5). In this work, we shall adhere to the optical terminology, which will be elaborated in §8 with emphasis on points of intersection with acoustic theory.

In communication, the concept of coherence has a narrower scope, even though the wave theoretical coherence from optics applies just as well. Coherent detection implies that there is a local oscillator that is capable of synchronizing (phase locking) to an external carrier. Once the internal and external oscillations are synchronized, they are effectively coherent as well, just as in optical coherence theory. We shall retain the communication jargon of “noncoherent” only in the context of communication reception and modulation detection, but refer to “incoherent” signals in other, more general contexts.

The psychoacoustic and neurophysiological definitions of coherence are looser, but appear to be synonymous with comodulation of the envelope domain of different bands of a broadband input. In order for it to coincide with the optical theory, the stimulus has to be demodulated first as a multi-carrier signal, so that each channel is demodulated independently, and the outputs from the different channels are used as inputs to the coherence function. In the brain, the latter operation is thought to be accomplished using coincidence detectors, which perform an instantaneous cross-correlation operation in neurons with multiple inputs (see §8.5). In this text, we generally refrain from using the term “coherence” if it refers to the envelope domain only, unless it is made explicit.

Similarly, neural synchrony can be recorded in different time scales. Synchronization (phase locking) to carrier frequencies takes place at low frequencies (estimated to be \(<\) 4–5 kHz in humans, §9.7.2). In higher-frequency channels, only slow-varying modulation information can be synchronized to. Low-frequency channels can be tracked both in the carrier and in the modulation domains. However, in the strict communication theory usage of the term, only the carrier tracking is real synchronization. We will nevertheless resort to talking about “envelope synchronization”, if only to to distinguish it from carrier phase locking.

What the brain theory and its auditory variations give us, which the wave theories do not, is the insight that synchronization can be linked to object formation and to selective attention. In other words, if these theories are correct, then synchronization to the stimulus on different levels in the brain may imply that it is being actively perceived, or is in attentional focus.

Cascading all these coherences into a continuous chain of processes, we see how coherence may propagate from the physical source of waves, through the medium, into the auditory system, and culminating in the conscious brain. As the brain processing speed is limited to low frequencies, it may not be able to fully synchronize to arbitrary stimuli, but there can still be low-frequency components that are tracked in the brain. Some of these points will be revisited in the chapter about the auditory phase locked loop (§9).

Footnotes

65. This expression is identical to the definition of modulation depth in amplitude modulation that is often used in auditory stimuli, Eq. §6.33.

66. These conditions entail that at light frequencies (of the order of \(10^{14}\) Hz) the electromagnetic wave would require umpteen periods to lose its degree of coherence.

67. Cook et al. (1955) cited S. G. Hershman, Zhur. Tekh. Fiz. 21, 1492 (1951), who originated the idea to use cross-correlation measures in acoustics.

68. Handel (2006) dedicated an entire book to “perceptual coherence” in visual and auditory phenomena, where commonalities in the processing of the two are contrasted. Unfortunately, the term is not explicitly defined in that work and seems to be used in more than one meaning throughout the book, which makes it difficult to exactly state what it means. It appears to measure how clearly mental objects are perceived—how sharp, differentiated from their surroundings, or stable they are.

69. The binding problem refers to the computational task of producing unified perceptual objects from various features that are recognized using different circuits (e.g., color, shape, location). The task often takes place in several modalities simultaneously—each with its own characteristic processing time. Binding is generally attributed to the cortex.

70. This point was made by the unnamed translator in the “Translator's Preface” of Duffieux (1983).

References

Barbour, Dennis L and Wang, Xiaoqin. Temporal coherence sensitivity in auditory cortex. Journal of Neurophysiology, 88 (5): 2684–2699, 2002.

Bertolotti, Mario, Ferrari, Aldo, and Sereda, Leonid. Coherence properties of nonstationary polychromatic light sources. Journal of the Optical Society of America B, 12 (2): 341–347, 1995.

Born, Max, Wolf, Emil, Bhatia, A. B., Clemmow, P. C., Gabor, D., Stokes, A. R., Taylor, A. M., Wayman, P. A., and Wilcock, W. L. Principles of Optics. Cambridge University Press, 7th (expanded) edition, 2003.

Bregman, Albert S. Auditory Scene Analysis: The Perceptual Organization of Sound. MIT press, 1990.

Cherry, E Colin and Sayers, Bruce Mc A. "human 'cross-correlator'"�—a technique for measuring certain parameters of speech perception. The Journal of the Acoustical Society of America, 28 (5): 889–895, 1956.

Cook, Richard K, Waterhouse, RV, Berendt, RD, Edelman, Seymour, and Thompson Jr, MC. Measurement of correlation coefficients in reverberant sound fields. The Journal of the Acoustical Society of America, 27 (6): 1072–1077, 1955.

Couch II, Leon W. Digital and Analog Communication Systems. Pearson Education Inc., Upper Saddle River, NJ, 8th edition, 2013.

Derode, Arnaud and Fink, Mathias. The notion of coherence in optics and its application to acoustics. European journal of physics, 15 (2): 81, 1994.

Dilhac, Jean-marie. Edouard Branly, the coherer, and the Branly effect. IEEE Communications Magazine, 47 (9): 20–26, 2009.

Duffieux, P. M. The Fourier Transform and Its Applications to Optics. John Wiley & Sons, 2nd edition, 1983. Translated from French, “L'intégrale de Fourier et ses applications á l'optique”, Masson, Editeur, Paris, 1970. First published in 1946.

Elhilali, Mounya, Ma, Ling, Micheyl, Christophe, Oxenham, Andrew J, and Shamma, Shihab A. Temporal coherence in the perceptual organization and cortical representation of auditory scenes. Neuron, 61 (2): 317–329, 2009.

Elhilali, Mounya. Modeling the cocktail party problem. In Middlebrooks, John C, Simon, Jonathan Z, Popper, Arthur N, and Fay, Richard R, editors, The Auditory System at the Cocktail Party, pages 111–135. ASA Press / Springer International Publishing AG, 2017.

Garratt, G. R. M. The Early History of Radio: from Faraday to Marconi. The Institution of Engineering and Technology, London, United Kingdom, 2006.

Goodman, Joseph W. Statistical optics. John Wiley & Sons, Inc., Hoboken, NJ, 2nd edition, 2015.

Handel, Stephen. Perceptual Coherence: Hearing and Seeing. Oxford University Press, New York, NY, 2006.

Ishimaru, Akira. Wave Propagation and Scattering in Random Media: Single Scattering and Transport Theory, volume 1. Academic Press, Inc., New York, NY, 1978a.

Ishimaru, Akira. Wave Propagation and Scattering in Random Media: Multiple Scattering, Turbulence, Rough Surfaces, and Remote Sensing, volume 2. Academic Press, Inc., New York, NY, 1978b.

Jeffress, Lloyd A, Blodgett, Hugh C, and Deatherage, Bruce H. Effect of interaural correlation on the precision of centering a noise. The Journal of the Acoustical Society of America, 34 (8): 1122–1123, 1962.

Jenkins, Gwilym M. and Watts, Donald G. Spectral Analysis and its Applications. Holden-Day, Inc., San Francisco, CA, 1968.

Lachaux, Jean-Philippe, Rodriguez, Eugenio, Martinerie, Jacques, and Varela, Francisco J. Measuring phase synchrony in brain signals. Human Brain Mapping, 8 (4): 194–208, 1999.

Lajunen, Hanna, Vahimaa, Pasi, and Tervo, Jani. Theory of spatially and spectrally partially coherent pulses. Journal of the Optical Society of America A, 22 (8): 1536–1545, 2005.

Lawson, James L. and Uhlenbeck, George E. Threshold Signals. McGraw-Hill Book Company, Inc., 1950.

Licklider, J. C. R. The influence of interaural phase relations upon the masking of speech by white noise. The Journal of the Acoustical Society of America, 20 (2): 150–159, 1948.

Malsburg, Christoph von der. The correlation theory of brain function (Internal Report 81-2). Technical report, Göettingen: Department of Neurobiology, Max Planck Institute for Biophysical Chemistry, 1981.

Malsburg, Ch. von der and Schneider, W. A neural cocktail-party processor. Biological Cybernetics, 54 (1): 29–40, 1986.

McAdams, Stephen. Spectral fusion, spectral parsing and the formation of auditory images. PhD thesis, Stanford University, 1984.

Milner, Peter M. A model for visual shape recognition. Psychological review, 81 (6): 521, 1974.

Morse, Philip M. and Ingard, K. Uno. Theoretical Acoustics. Princeton University Press, Princeton, NJ, 1968.

Morse, Philip M and Bolt, Richard H. Sound waves in rooms. Reviews of Modern Physics, 16 (2): 69, 1944.

Nelken, Israel, Rotman, Yaron, and Yosef, Omer Bar. Responses of auditory-cortex neurons to structural features of natural sounds. Nature, 397 (6715): 154–157, 1999.

van Noorden, L. P. A. S. Temporal Coherence in the Perception of Tone Sequences. PhD thesis, Technische Hogeschool Eindhoven, 1975.

Paez, Thomas L. The history of random vibrations through 1958. Mechanical Systems and Signal Processing, 20 (8): 1783–1818, 2006.

Schroeder, Manfred Robert. Frequency-correlation functions of frequency responses in rooms. The Journal of the Acoustical Society of America, 34 (12): 1819–1823, 1962.

Schuster, Arthur. An Introduction to the Theory of Optics. Edward Arnold, London, 2nd revised edition, 1909.

Senkowski, Daniel, Schneider, Till R, Foxe, John J, and Engel, Andreas K. Crossmodal binding through neural coherence: Implications for multisensory processing. Trends in Neurosciences, 31 (8): 401–409, 2008.

Sereda, Leonid, Bertolotti, Mario, and Ferrari, Aldo. Coherence properties of nonstationary light wave fields. Journal of the Optical Society of America A, 15 (3): 695–705, 1998.

Shamma, Shihab A, Elhilali, Mounya, and Micheyl, Christophe. Temporal coherence and attention in auditory scene analysis. Trends in Neurosciences, 34 (3): 114–123, 2011.

Shin, Kihong and Hammond, Joseph. Fundamentals of Signal Processing for Sound and Vibration Engineers. John Wiley & Sons, West Sussex, England, 2008.

Singer, Wolf and Gray, Charles M. Visual feature integration and the temporal correlation hypothesis. Annual Review of Neuroscience, 18 (1): 555–586, 1995.

Tatarskii, Valerian Ilitch. The Effects of the Turbulent Atmosphere on Wave Propagation. Israel Program for Scientific Translations, Jerusalem, 1971.

van Cittert, Pieter Hendrik. Die wahrscheinliche schwingungsverteilung in einer von einer lichtquelle direkt oder mittels einer linse beleuchteten ebene. Physica, 1 (1-6): 201–210, 1934.

van Cittert, PH. Kohaerenz-probleme. Physica, 6 (7-12): 1129–1138, 1939.

Varela, Francisco, Lachaux, Jean-Philippe, Rodriguez, Eugenio, and Martinerie, Jacques. The brainweb: phase synchronization and large-scale integration. Nature Reviews Neuroscience, 2 (4): 229–239, 2001.

Verdet, Emile. Étude sur la constitution de la lumiere non polarisée et de la lumiere partiellement polarisée. Annales Scientifiques de l'École Normale Supérieure, 2: 291–316, 1865.

Viswanathan, Vibha, Shinn-Cunningham, Barbara G., and Heinz, Michael G. Speech categorization reveals the role of early-stage temporal-coherence processing in auditory scene analysis. Journal of Neuroscience, 42 (2): 240–254, 2022.

Viterbi, Andrew J. and Omura, Jim K. Principles of Digital Communication and Coding. McGraw-Hill, Inc., New York, NY, 1979.

Wiener, Norbert. Coherency matrices and quantum. Journal of Mathematics and Physics, 7 (1-4): 109–125, 1928.

Wiener, Norbert. Generalized harmonic analysis. Acta Mathematica, 55: 117–258, 1930.

Wolf, E. A macroscopic theory of interference and diffraction of light from finite sources, I. Fields with a narrow spectral range. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 225 (1160): 96–111, 1954.

Wolf, Emil. A macroscopic theory of interference and diffraction of light from finite sources II. Fields with a spectral range of arbitrary width. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 230 (1181): 246–265, 1955.

Wolf, Emil. New theory of partial coherence in the space–frequency domain. part I: Spectra and cross spectra of steady-state sources. Journal of the Optical Society of America, 72 (3): 343–351, 1982.

Wolf, Emil. New theory of partial coherence in the space-frequency domain. part II: Steady-state fields and higher-order correlations. Journal of the Optical Society of America A, 3 (1): 76–85, 1986.

Toraldo di Francia, G. Capacity of an optical channel in the presence of noise. Optica Acta: International Journal of Optics, 2: 5–8, 1955.